Công thức tính diện tích hình thoi đơn giản, dễ áp dụng

Hình thoi là một hình học cơ bản trong chương trình Toán tiểu học, tuy nhiên không phải ai cũng biết cách tính diện tích của nó. Để củng cố kiến thức về toán học, bạn có thể tham khảo bài viết này để hiểu rõ về khái niệm hình thoi và công thức tính diện tích của nó. Với các ví dụ minh họa, bạn sẽ dễ dàng giải quyết mọi bài toán từ đơn giản đến phức tạp về hình thoi.

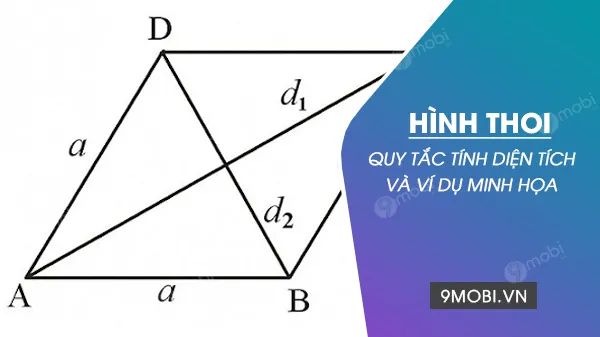
Công thức chuẩn để tính diện tích hình thoi

I. Khái niệm hình thoi là gì?

Hình thoi là tứ giác có bốn cạnh đồng đều. Cách đơn giản nhất để hiểu, hình thoi là một loại hình bình hành có hai cạnh kề bằng nhau và hai đường chéo vuông góc với nhau.

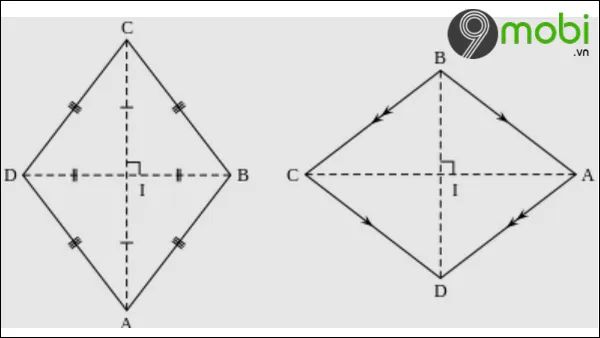
II. Quy tắc tính diện tích hình thoi cùng ví dụ dễ hiểu

1. Công thức tính diện tích hình thoi

Diện tích hình thoi được tính bằng một nửa tích của độ dài hai đường chéo.

Công thức tính diện tích hình thoi là:

S = 1/2 x (d1 x d2)

Hoặc S = h x a

Trong đó:

- S: Là diện tích của hình thoi.

- d1, d2: Là độ dài của hai đường chéo của hình thoi.

- h: Là chiều cao của hình thoi, tính từ đáy đến đỉnh đối diện.

- a: Là độ dài của cạnh hình thoi.

2. Giải bài tập tính diện tích hình thoi cho học sinh lớp 4, 5

Với công thức tính diện tích hình thoi bằng nửa tích của hai đường chéo, chúng ta có thể phát triển nhiều phương pháp tính diện tích khác nhau. Cụ thể như sau:

2.1. Tính diện tích hình thoi qua hai đường chéo

Phương pháp giải: Bạn cần xác định chiều dài của hai đường chéo và áp dụng công thức: S = 1/2 x (d1 x d2).

2.2. Tính diện tích hình thoi qua chiều cao và cạnh đáy

Phương pháp giải: Bạn cần xác định chiều cao và cạnh đáy của hình thoi, sau đó áp dụng công thức: S = a x h để tính diện tích.

2.3. Tính diện tích hình thoi theo công thức lượng giác

Phương pháp giải: Xét hình thoi ABCD, gọi độ dài cạnh là a. Áp dụng công thức lượng giác: S = a² x sin(α) để tính diện tích hình thoi bất kỳ.

Lưu ý:

- S: Đại diện cho diện tích của hình thoi.

- a: Độ dài của cạnh hình thoi.

- α: Là góc của hình thoi, đo một góc bất kỳ trong đó.
 

3. Ví dụ về công thức và cách tính diện tích hình thoi

Để giúp bạn đọc và học sinh hiểu rõ hơn về cách tính diện tích hình thoi, Tripi sẽ giới thiệu một số ví dụ cụ thể sau đây.

Bài toán 1: Có một cánh diều hình thoi với hai đường chéo giao nhau có độ dài lần lượt là 6cm và 8cm. Hỏi diện tích của cánh diều này là bao nhiêu?

Giải:

Đặt d1, d2 lần lượt là độ dài của hai đường chéo của cánh diều, ta có d1 = 6cm và d2 = 8cm.

Áp dụng công thức diện tích hình thoi S = 1/2 x (d1 x d2), ta tính được diện tích cánh diều hình thoi như sau:

S = 1/2 x (6 x 8) = 1/2 x 48 = 24 (cm²).

Bài toán 2: Cho hình thoi ABCD với cạnh a = 4cm, góc A = 35 độ. Tính diện tích của hình thoi.

Giải:

Theo đề bài, ta có a = 4cm, góc A = 35 độ.

Áp dụng công thức lượng giác, ta tính được diện tích: S = a² x sin(A) = 4² x sin(35) = 9,176 (cm²).

Bài toán 3: Cho một hình thoi có cạnh đáy dài 10 cm và chiều cao 7 cm. Tính diện tích của hình thoi này?

Giải:

Theo đề bài, ta có h = 7cm và a = 10cm. Áp dụng công thức diện tích hình thoi S = a x h, ta tính được diện tích:

S = 7 x 10 = 70 (cm²).

Vậy, với quy tắc tính diện tích hình thoi mà Tripi đã chia sẻ, các bài toán về hình thoi sẽ không còn là thử thách đối với bạn. Chúc các bạn học tốt!

https://Tripi.vn/quy-tac-tinh-dien-tich-hinh-thoi-de-hieu-nhanh-32150n.aspx
Như đã đề cập, hình thoi là một dạng đặc biệt của hình bình hành. Để dễ dàng phân biệt và ghi nhớ cách tính chu vi, diện tích của cả hai loại hình học này, bạn có thể tham khảo thêm cách tính diện tích hình bình hành mà Tripi.vn đã tổng hợp và chia sẻ.