Hướng dẫn chi tiết cách tính chu vi hình đa giác

Sau khi đã quen với các hình cơ bản như tam giác, vuông, chữ nhật, học sinh tiểu học sẽ bắt đầu làm quen với những hình phức tạp hơn – đó chính là hình đa giác.

Hình đa giác là gì? Có mấy loại hình đa giác? Phương pháp tính chu vi của chúng ra sao? Tất cả sẽ được làm rõ trong nội dung sau đây từ Tripi.vn.

Phương pháp tính chu vi hình đa giác

1. Cách tính chu vi hình đa giác chi tiết và dễ hiểu

Hình đa giác là một đường gấp khúc khép kín, được tạo nên bởi các đoạn thẳng liên tiếp nối nhau sao cho điểm đầu trùng với điểm cuối.

Để hiểu sâu hơn về khái niệm và đặc điểm các loại đa giác, bạn có thể tham khảo thêm trên Wiki Tại Đây.

Dựa trên số cạnh và hình dạng của các cạnh, đa giác được phân chia thành ba nhóm chính: đa giác đều, đa giác lồi và đa giác lõm.

Chu vi của hình đa giác là tổng độ dài các cạnh cấu thành nên hình, chính là đường bao quanh toàn bộ hình đó.

- Công thức tính chu vi đa giác: P = a1 + a2 + a3 + ... + an

Trong đó:

P biểu thị chu vi của hình đa giác

a1, a2, a3,..., an lần lượt là các cạnh tạo thành hình đa giác

Công thức trên là công thức tổng quát, có thể áp dụng cho mọi loại đa giác, từ đa giác đều cho đến đa giác không đều.

Ví dụ minh họa: Tính chu vi đa giác không đều

Bài tập 1: Tính chu vi của ngũ giác ABCDF biết độ dài các cạnh lần lượt là 12, 13, 28, 6 và 19 đơn vị

Lời giải chi tiết

Áp dụng công thức tính chu vi hình đa giác, ta có:

- Chu vi của ngũ giác ABCDF là: P(ABCDF) = 12 + 13 + 28 + 6 + 19 = 78 cm

2. Công thức tính chu vi của hình đa giác đều

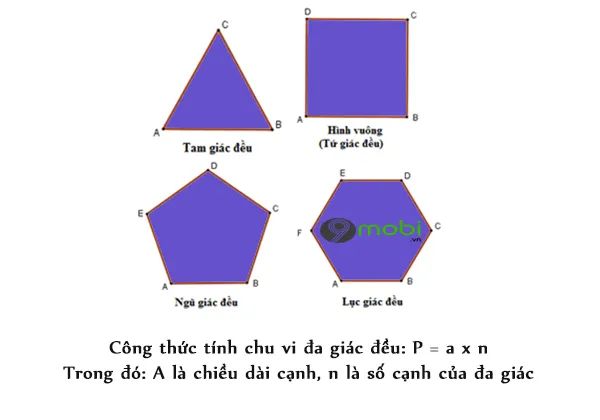
- Khái niệm: Hình đa giác đều là hình có tất cả các cạnh và các góc ở đỉnh bằng nhau. Một số ví dụ điển hình: tam giác đều (3 cạnh), hình vuông (4 cạnh), ngũ giác đều (5 cạnh), lục giác đều (6 cạnh)...

- Chu vi hình đa giác đều: Do tính chất đồng đều giữa các cạnh và góc, việc tính chu vi của hình đa giác đều trở nên đơn giản và nhanh chóng.

Công thức tính chu vi đa giác đều: P = a × n

Giải thích các ký hiệu:

P đại diện cho chu vi của đa giác đều

a là độ dài mỗi cạnh của đa giác

n thể hiện số lượng cạnh của đa giác

Ví dụ 2: Tính chu vi hình vuông ABCD với độ dài mỗi cạnh là 12 cm

Lời giải chi tiết:

Áp dụng công thức chu vi đa giác đều, chu vi hình vuông ABCD được tính như sau: P(ABCD) = 12 x 4 = 48 cm

Ví dụ 3: Tìm độ dài cạnh của lục giác đều ABCDEF khi biết chu vi là 108 cm

Lời giải:

Dựa trên dữ liệu đã cho, ta có các thông tin sau:

Theo công thức chu vi đa giác đều, ta có: P(ABCDEF) = 6 x AB = 108 cm

Suy ra độ dài mỗi cạnh AB = 18 cm

Lục giác đều ABCDEF gồm 6 cạnh bằng nhau, do đó AB = BC = CD = DE = EF = FA = 18 cm

Đáp án: Độ dài một cạnh của lục giác đều là 18 cm

Trên đây là ví dụ minh họa cho cách tính chu vi đa giác không đều và đa giác đều. Với các bài toán yêu cầu hai cách tính chu vi, bạn có thể sử dụng công thức chung hoặc phân chia đa giác thành các hình nhỏ hơn để tính tổng chu vi các phần đó.

Bài viết từ Tripi.vn đã hướng dẫn chi tiết cách tính chu vi các hình đa giác đều và không đều. Khi đã hiểu rõ các công thức tính chu vi của tam giác, hình chữ nhật, hình vuông,... thì việc áp dụng với đa giác sẽ trở nên dễ dàng hơn bao giờ hết.

https://Tripi.vn/cach-tinh-chu-vi-da-giac-25728n.aspx
Hình thoi là một dạng đa giác đều với bốn cạnh bằng nhau và đối diện song song. Công thức tính chu vi hình thoi tương tự như công thức tính chu vi đa giác đều. Để khám phá kỹ hơn về cách tính chu vi hình thoi, bạn đọc có thể tham khảo bài viết chi tiết tại Tripi.vn.