Công thức tính đường chéo hình lập phương và ví dụ minh họa
Nội dung bài viết
Bài viết này sẽ cung cấp cho bạn công thức tính đường chéo hình lập phương cùng với các ví dụ minh họa chi tiết.

I. Giới thiệu về hình lập phương
Hình lập phương là một khối hình học ba chiều, được tạo thành từ sáu mặt vuông đồng nhất, mỗi mặt đều có diện tích và hình dạng giống nhau. Còn được gọi là khối lập phương hoặc hình khối đều, mỗi mặt của hình lập phương là một hình vuông với độ dài cạnh bằng nhau, ký hiệu là “a”. Diện tích một mặt là a², diện tích toàn phần là 6a², và thể tích được tính bằng công thức a³.

II. Khái niệm và công thức tính đường chéo hình lập phương
1. Khái niệm đường chéo hình lập phương
Đường chéo của hình lập phương là đoạn thẳng nối hai đỉnh không cùng nằm trên một cạnh. Nó cũng có thể được hiểu như đường chéo của một hình tứ diện đều, bởi hình lập phương cũng là một dạng đặc biệt của tứ diện đều.
2. Công thức tính đường chéo hình lập phương
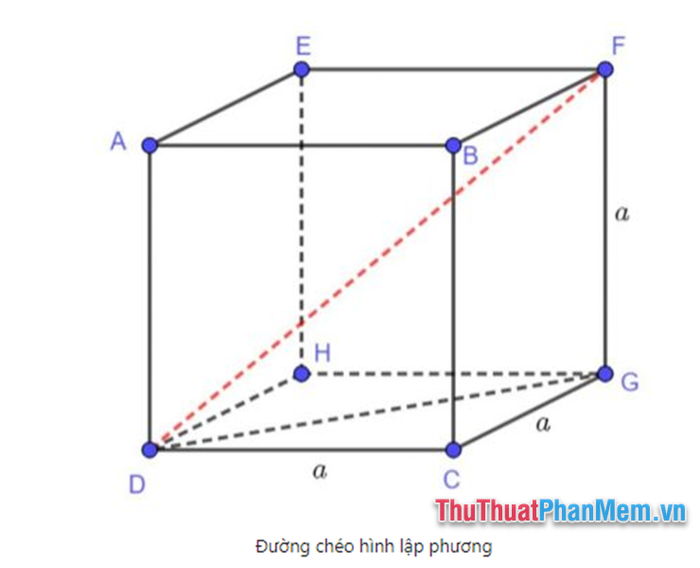
Trong hình lập phương ABCD.A’B’C’D’ với các cạnh đều có độ dài bằng a, áp dụng định lý Pitago, ta có thể tính được đường chéo của một mặt như sau:
Đường chéo AC của mặt ABCD = a√2
Đường chéo của hình lập phương được tính bằng công thức AC’ = √(AC² + CC’²) = √(2a² + a²) = a√3
Có hai công thức phổ biến để tính độ dài đường chéo trong hình lập phương, mang lại sự linh hoạt và chính xác trong tính toán.
+ Công thức tính độ dài đường chéo hình lập phương: D = a√3
+ Công thức tính độ dài đường chéo mặt bên hình lập phương: d = a√2
Ký hiệu trong công thức tính đường chéo hình lập phương bao gồm:
- a: Độ dài cạnh của hình lập phương
- D: Đường chéo hình lập phương
- d: Đường chéo mặt bên hình lập phương
3. Ví dụ minh họa
Cho hình lập phương có độ dài cạnh a = 3cm. Hãy tính độ dài đường chéo của hình lập phương đó.
Lời giải:
Theo ký hiệu trên hình vẽ, AC là đường chéo của mặt vuông ABCD, và AC’ là đường chéo của toàn bộ hình lập phương ABCD.A’B’C’D’.
Xét tam giác ABC vuông tại B:
AB² + BC² = AC²
⇔ 3² + 3² = AC²
⇔ 18 = AC²
=> AC = 3√2 (cm)
Vì ABCD.A’B’C’D’ là hình lập phương nên CC' vuông góc với mặt phẳng (ABCD).
=> CC' vuông góc với AC
Xét tam giác ACC', ta có:
AC² + CC'² = AC'²
⇔ (3√2)² + 3² = AC'²
⇔ 27 = AC'²
=> AC' = 3√3 (cm)
Trên đây là những chia sẻ chi tiết về công thức tính đường chéo hình lập phương cùng ví dụ minh họa. Hy vọng bài viết đã mang đến cho bạn những kiến thức bổ ích. Chúc bạn một ngày tràn đầy niềm vui!
Có thể bạn quan tâm

Top 5 Trường mầm non quốc tế chất lượng nhất tại quận Hà Đông, Hà Nội

Nước Xịt Khoáng Evoluderm: Lợi Ích, Giá Cả Và Nơi Mua

Top 10 mẫu máy lạnh và điều hòa được ưa chuộng nhất cho mùa hè

Top 5 viên ngậm trắng da hiệu quả hàng đầu hiện nay

Cung Nhân Mã thuộc tháng mấy? Khám phá tính cách và chuyện tình yêu đặc trưng của chòm sao Nhân Mã


