Công thức tính thể tích khối lăng trụ và các ví dụ minh họa

Tính thể tích khối lăng trụ là một dạng toán phổ biến trong hình học không gian, đồng thời có nhiều ứng dụng thực tiễn trong đời sống. Nếu bạn chưa nắm rõ công thức, hãy cùng khám phá công thức tính thể tích khối lăng trụ và các ví dụ cụ thể được Tripi chia sẻ dưới đây.

1. Khối lăng trụ là gì?

Hình lăng trụ là hình học có hai đáy là đa giác bằng nhau, các mặt bên là hình bình hành với các cạnh song song hoặc bằng nhau. Đáy của hình lăng trụ có thể là tam giác, tứ giác hoặc bất kỳ đa giác nào khác. Tên gọi của hình lăng trụ được xác định dựa trên hình dạng đáy, ví dụ: lăng trụ tam giác, lăng trụ tứ giác.

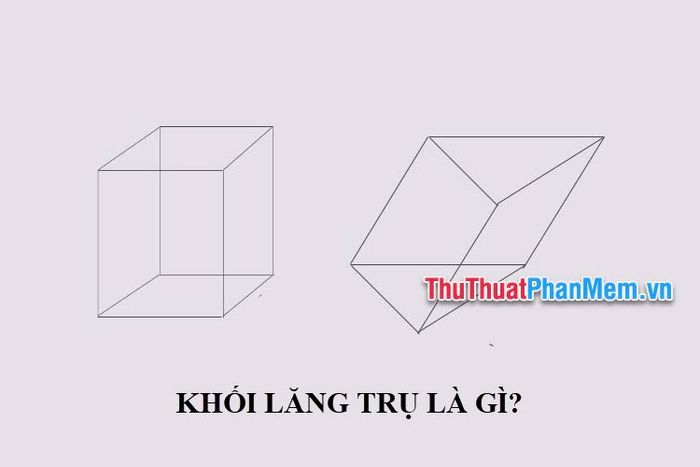
Khối lăng trụ là phần không gian được bao bọc bởi một hình lăng trụ, bao gồm cả hình lăng trụ đó. Tên gọi của khối lăng trụ được xác định dựa trên hình dạng của hình lăng trụ tương ứng.

2. Một số dạng hình lăng trụ phổ biến

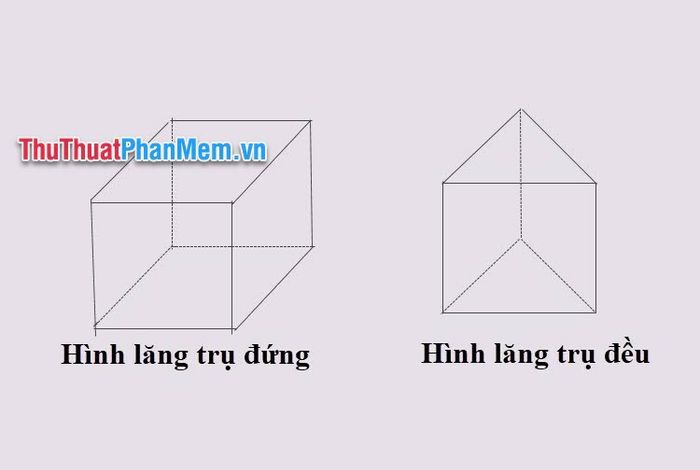
• Hình lăng trụ đứng: Là hình lăng trụ có các cạnh bên vuông góc với mặt đáy, độ dài cạnh bên chính là chiều cao của hình. Các mặt bên của hình lăng trụ đứng đều là hình chữ nhật.
• Hình lăng trụ đều: Là hình lăng trụ đứng có đáy là đa giác đều. Các mặt bên của lăng trụ đều là những hình chữ nhật bằng nhau.

• Hình hộp: Là hình lăng trụ có đáy là hình bình hành.
• Hình hộp đứng: Là hình lăng trụ đứng có đáy là hình bình hành.
• Hình hộp chữ nhật: Là hình lăng trụ đứng với các mặt bên đều là hình chữ nhật.
• Hình lập phương: Là hình lăng trụ đứng có đáy là hình vuông và các mặt bên cũng là hình vuông.

3. Công thức tính thể tích hình lăng trụ

Thể tích của hình lăng trụ đứng được xác định bằng tích của diện tích mặt đáy và chiều cao (khoảng cách giữa hai mặt đáy).

Công thức tính thể tích hình lăng trụ: V = A x h

Trong đó:

• V là thể tích của khối lăng trụ
• A là diện tích mặt đáy của khối lăng trụ
• h là chiều cao của khối lăng trụ

4. Ví dụ minh họa tính thể tích khối lăng trụ

Ví dụ 1: Cho khối lăng trụ đứng có đáy là hình vuông với độ dài cạnh 4 cm và chiều cao 6 cm. Hãy tính thể tích của khối lăng trụ này.

Lời giải

Tính diện tích mặt đáy của khối lăng trụ:

A = 4² = 16 cm²

Áp dụng công thức tính thể tích khối lăng trụ, ta được:

V = A x h = 16 x 6 = 96 cm³

Vậy thể tích của khối lăng trụ là 96 cm³

Ví dụ 2: Cho hình lăng trụ tam giác đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a, đường chéo mặt bên $A{B}^{\prime }=a\sqrt{2}$. Hãy tính thể tích khối lăng trụ ABC.A’B’C’.

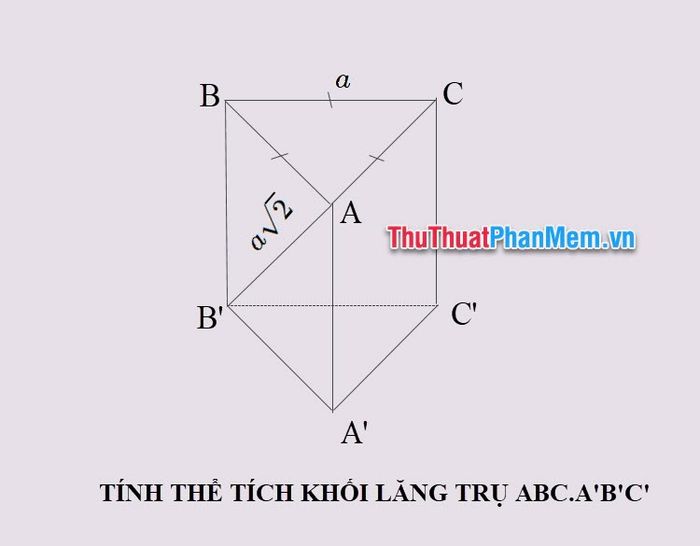
Lời giải

Xét tam giác vuông ABB’ tại B, ta có $A{B}^{\prime }=a\sqrt{2}$ và AB = a.

Áp dụng định lý Pytago, ta có:

$B{B}^{\prime }=\sqrt{A{B}^{\prime 2}-A{B}^2}=\sqrt{(a\sqrt{2}{)}^2-a^2}=a$

Diện tích tam giác đáy $S_{ABC}=\frac{a^2\sqrt{3}}{4}$

Áp dụng công thức tính thể tích khối lăng trụ, ta được:

Thể tích của khối lăng trụ được tính bằng công thức: V=SABC×BB′=a2√34×a2=a3√34$V=S_{ABC}\times B{B}^{\prime }=\frac{a^2\sqrt{3}}{4}\times a^2=\frac{a^3\sqrt{3}}{4}$

Kết quả cuối cùng, thể tích của khối lăng trụ là a3√34$\frac{a^3\sqrt{3}}{4}$

Tripi đã chia sẻ cùng bạn công thức tính thể tích khối lăng trụ kèm ví dụ minh họa. Hy vọng rằng những kiến thức này sẽ giúp bạn hiểu rõ hơn về cách tính thể tích khối lăng trụ, từ đó áp dụng linh hoạt vào việc giải quyết các bài toán liên quan. Cảm ơn bạn đã dành thời gian theo dõi và ủng hộ bài viết!