Khám phá công thức Heron - Phương pháp tính diện tích tam giác chính xác từ ba cạnh

Bạn đang tìm hiểu về công thức Heron để tính diện tích tam giác khi biết độ dài ba cạnh? Hãy cùng khám phá bài viết dưới đây để nắm vững cách áp dụng công thức Heron một cách hiệu quả.

Bài viết dưới đây sẽ giới thiệu chi tiết công thức Heron và hướng dẫn cách tính diện tích tam giác dựa trên độ dài ba cạnh. Mời bạn cùng theo dõi và áp dụng.

Công thức Heron là một phương pháp tính diện tích tam giác dựa trên độ dài ba cạnh, được đặt theo tên nhà toán học nổi tiếng Heron của Alexandria.

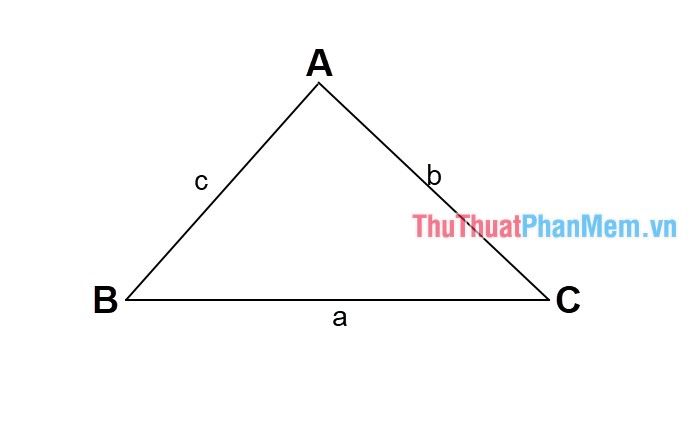
Công thức Heron được biểu diễn một cách tinh tế như sau:

Gọi S là diện tích tam giác, với độ dài ba cạnh lần lượt là a, b và c.

S=√p(p−a)(p−b)(p−c)$S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$

Trong đó, p là nửa chu vi của tam giác, một yếu tố quan trọng trong công thức.

p=a+b+c2$p=\frac{a+b+c}{2}$

Công thức Heron còn có thể được biểu diễn một cách tinh tế hơn như sau:

S=√(a+b+c)(a+b−c)(b+c−a)(c+a−b)4$S=\frac{\sqrt{\left(a+b+c\right)\left(a+b-c\right)\left(b+c-a\right)\left(c+a-b\right)}}{4}$

S=√2(a2b2+a2c2+b2c2)−(a4+b4+c4)4$S=\frac{\sqrt{2\left(a^2{b}^2+a^2{c}^2+b^2{c}^2\right)-\left(a^4+b^4+c^4\right)}}{4}$

S=√(a2+b2+c2)2−2(a4+b4+c4)4$S=\frac{\sqrt{{\left(a^2+b^2+c^2\right)}^2-2\left(a^4+b^4+c^4\right)}}{4}$

Phương pháp chứng minh công thức Heron

Phương pháp chứng minh này kết hợp tinh tế giữa đại số và lượng giác.

Gọi a, b, c lần lượt là ba cạnh của tam giác và A, B, C là các góc đối diện tương ứng. Theo hệ quả của định lý cosin, ta có:

cos(C)=a2+b2−c22ab$\cos \left(C\right)=\frac{a^2+b^2-c^2}{2ab}$

Từ đây, ta suy ra:

sin(C)=√1−cos2(C)=√4a2b2−(a2+b2−c2)22ab$\sin \left(C\right)=\sqrt{1-{\cos }^2\left(C\right)}=\frac{\sqrt{4a^2{b}^2-{\left(a^2+b^2-c^2\right)}^2}}{2ab}$

Dựa vào đường cao và giá trị sin của góc C, ta có thể suy ra công thức tính diện tích tam giác ABC một cách chính xác.

Nếu bạn muốn tính diện tích tam giác với ba cạnh a, b, c, trước tiên hãy tính nửa chu vi của tam giác theo công thức sau:

p=a+b+c2$p=\frac{a+b+c}{2}$

Sau đó, áp dụng công thức Heron để tính diện tích tam giác một cách chính xác:

S=√p(p−a)(p−b)(p−c)$S=\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}$

Trên đây là công thức Heron và cách áp dụng để tính diện tích tam giác một cách hiệu quả. Hy vọng bài viết đã mang đến cho bạn những kiến thức bổ ích, giúp bạn nắm vững và ứng dụng công thức Heron một cách linh hoạt trong các bài toán hình học. Chúc bạn thành công và đạt được nhiều kết quả tốt đẹp!