Hàm LINEST - Công cụ Excel trả về mảng dữ liệu mô tả đường thẳng tối ưu thông qua phương pháp bình phương nhỏ nhất, hỗ trợ phân tích hồi quy chính xác.

Bài viết này giới thiệu hàm LINEST - một trong những hàm thống kê được sử dụng phổ biến và hiệu quả trong Excel.

Mô tả: Hàm LINEST trả về mảng dữ liệu mô tả đường thẳng dựa trên phương pháp bình phương nhỏ nhất, giúp tối ưu hóa phân tích dữ liệu.

Cú pháp: LINEST(known_y's, [known_x's], [const], [stats]) - Công thức mạnh mẽ để thực hiện phân tích hồi quy tuyến tính trong Excel.

Trong đó:

- known_y's: Tập hợp các giá trị y đã biết trong phương trình y = b*m^x, là tham số không thể thiếu.

+ Nếu known_y's nằm trong một cột hoặc hàng đơn lẻ, mỗi cột hoặc hàng sẽ được xem như một biến số độc lập.

- known_x's: Tập hợp các giá trị x đã biết trong phương trình y = b*m^x, là tham số tùy chọn nhưng mang lại sự linh hoạt trong phân tích.

+ known_x's có thể chứa một hoặc nhiều tập biến số, mang lại sự linh hoạt trong việc phân tích dữ liệu đa chiều.

+ Nếu known_x's không được cung cấp, hệ thống sẽ tự động giả định một mảng có kích thước tương đương với known_y's để đảm bảo tính nhất quán.

- const: Giá trị logic quyết định cách xử lý hằng số b trong phương trình, là tham số tùy chọn với các tùy biến sau:

+ const = True hoặc bỏ qua -> giá trị b sẽ được tính toán một cách tự nhiên và chính xác.

+ const = False hoặc bỏ qua -> giá trị b được đặt là 1 và hệ số m được điều chỉnh để phương trình trở thành: y = m^x, tối ưu hóa mô hình.

- stats: Giá trị logic quyết định việc trả về các thống kê hồi quy bổ sung, bao gồm: {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r2,sey;F,df;ssreg,ssresid}, giúp phân tích sâu hơn về dữ liệu.

Chú ý:

- Mọi đường thẳng đều có thể được biểu diễn thông qua độ dốc và điểm giao cắt trục y, mang lại cái nhìn trực quan và dễ hiểu.

+ Độ dốc (m):

Để xác định độ dốc của đường thẳng, chọn hai điểm bất kỳ (x1, y1) và (x2, y2) trên đường thẳng, độ dốc được tính bằng công thức (y2 - y1)/(x2 - x1), thể hiện sự thay đổi của y theo x.

+ Giao cắt Y (b):

Giao cắt y của đường thẳng là giá trị y tại điểm mà đường thẳng đi qua trục tung, thể hiện giá trị của y khi x = 0, mang lại cái nhìn tổng quan về vị trí của đường thẳng trên hệ trục tọa độ.

Phương trình đường thẳng được biểu diễn bởi công thức y = mx + b. Bạn có thể dễ dàng tính toán bất kỳ điểm nào trên đường thẳng bằng cách thay giá trị y hoặc x vào phương trình này.

- Trong trường hợp chỉ có một biến độc lập, bạn có thể áp dụng công thức sau:

+ Độ dốc:

=INDEX(LINEST(known_y's,known_x's),1)

+ Giao cắt Y:

=INDEX(LINEST(known_y's,known_x's),2)

+ Sử dụng dấu phẩy để phân tách các giá trị trong cùng một hàng, giúp dữ liệu được tổ chức một cách rõ ràng và dễ hiểu.

+ Dùng dấu chấm phẩy để phân cách giữa các hàng với nhau, tạo nên sự liên kết logic và mạch lạc trong cấu trúc dữ liệu.

- Khi có nhiều biến độc lập x, bạn có thể áp dụng công thức sau để tính toán:

$m=\frac{\sum \left(x-\overline{x}\right)\left(y-\overline{y}\right)}{\sum {\left(x-\overline{x}\right)}^2}$

$b=\overline{y}-m\overline{x}$

Trong đó: x = AVERAGE(known_x's) và y = AVERAGE(known_y's), giúp xác định giá trị trung bình của các biến độc lập và phụ thuộc.

Ví dụ:

Tính toán độ dốc và giao cắt y của đường thẳng dựa trên các giá trị x, y được cung cấp trong bảng dữ liệu sau:

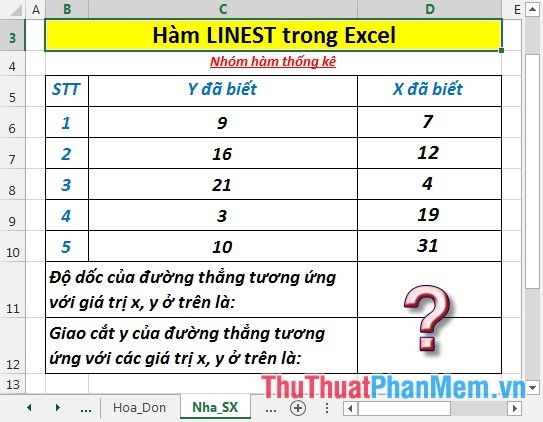
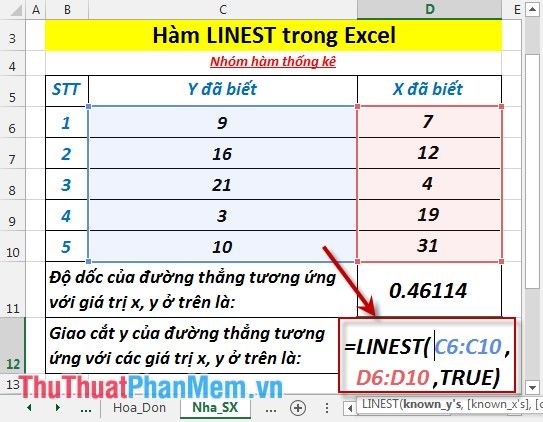
- Để tính độ dốc m của đường thẳng, nhập công thức sau vào ô cần tính: =LINEST(C6:C10,D6:D10,FALSE).

- Nhấn Enter để nhận kết quả, độ dốc m của đường thẳng tương ứng với các giá trị x, y sẽ được hiển thị.

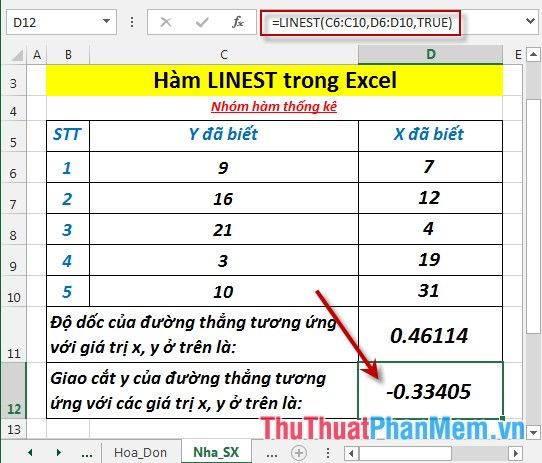
- Để tính giao cắt y của đường thẳng, nhập công thức sau vào ô cần tính: =LINEST(C6:C10,D6:D10,TRUE).

- Nhấn Enter để nhận kết quả, giao cắt y của đường thẳng tương ứng với các giá trị x, y sẽ được hiển thị.

Trên đây là hướng dẫn chi tiết và ví dụ minh họa cụ thể khi sử dụng hàm LINEST trong Excel, giúp bạn áp dụng hiệu quả vào công việc phân tích dữ liệu.

Chúc các bạn thành công và khám phá thêm nhiều ứng dụng thú vị của hàm LINEST trong Excel!