Hàm POISSON - Công cụ Excel mạnh mẽ để tính toán phân bố Poisson

Khi cần dự đoán số lượng sự kiện xảy ra trong một khoảng thời gian cụ thể, hàm POISSON là lựa chọn không thể bỏ qua. Bài viết này sẽ hướng dẫn chi tiết cách sử dụng hàm POISSON, giúp bạn hiểu rõ cách trả về phân bố Poisson trong Excel.

Mô tả: Hàm POISSON trả về phân bố Poisson, là công cụ hữu ích để xác định số sự kiện xảy ra trong một khoảng thời gian nhất định. Ví dụ, bạn có thể tính toán số xe qua trạm thu phí trong 1 phút dựa trên mật độ xe ngày cuối tuần. Từ đó, đưa ra các biện pháp hỗ trợ phù hợp.

Cú pháp: POISSON(x, mean, cumulative), trong đó x là số sự kiện, mean là giá trị trung bình kỳ vọng, và cumulative là giá trị logic xác định dạng phân bố.

Trong công thức hàm POISSON, các tham số được sử dụng như sau:

- x: Số sự kiện cần tính toán, đây là tham số bắt buộc không thể thiếu.

- mean: Giá trị trung bình kỳ vọng, được biểu diễn dưới dạng số và cũng là tham số bắt buộc.

- cumulative: Giá trị logic quyết định dạng thức của kết quả trả về, mang ý nghĩa quan trọng trong việc xác định phân bố.

+ Nếu cumulative = TRUE, hàm sẽ trả về xác suất Poisson lũy tích trong khoảng 0 < số sự kiện <= x.

+ Nếu cumulative = FALSE, hàm sẽ trả về xác suất Poisson lũy tích khi số sự kiện chính xác bằng x.

Lưu ý quan trọng:

- Công thức tính toán của hàm Poisson được xác định như sau:

+ Khi cumulative = TRUE:

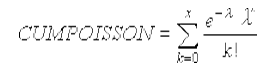
+ Khi cumulative = FALSE:

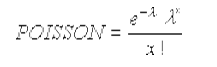
- Nếu giá trị của x là số thập phân, hàm sẽ tự động lấy phần nguyên của x để tính toán.

- Cả x và giá trị trung bình (mean) phải ở dạng số, nếu không hàm sẽ trả về lỗi #VALUE.

- Nếu giá trị của x nhỏ hơn 0, hàm sẽ trả về lỗi #NUM!.

- Nếu giá trị trung bình (mean) nhỏ hơn 0, hàm cũng sẽ trả về lỗi #NUM!.

Ví dụ minh họa:

- Tính toán phân bố Poisson khi cumulative = TRUE:

Tại ô cần tính toán, nhập công thức: =POISSON(D13,D14,D15).

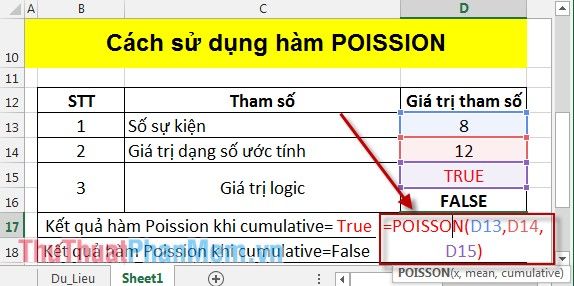
Nhấn Enter để nhận kết quả:

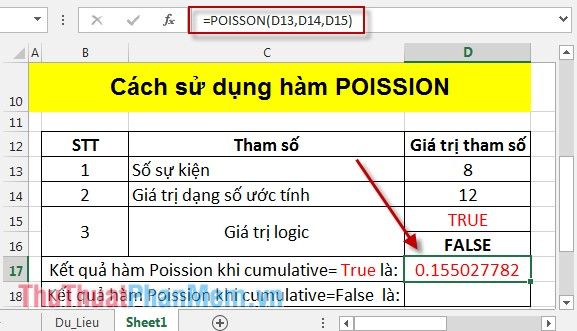
- Tính toán phân bố Poisson khi cumulative = FALSE:

Tại ô cần tính toán, nhập công thức: =POISSON(D13,D14,D16).

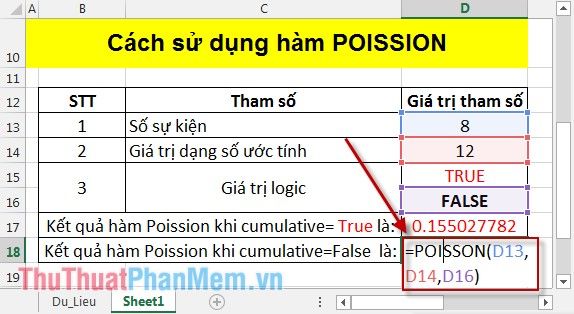
Nhấn Enter để nhận ngay kết quả:

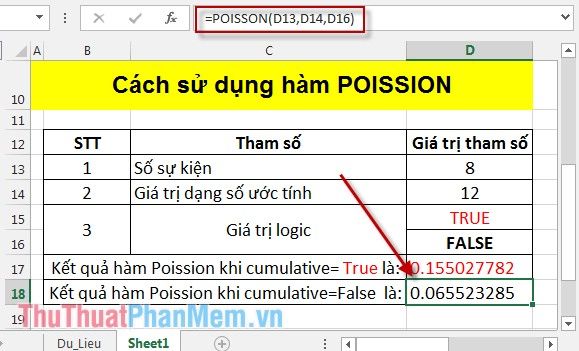
Như vậy, giá trị của hàm Poisson sẽ thay đổi tùy thuộc vào tham số cumulative. Hy vọng rằng hàm Poisson sẽ trở thành công cụ hữu ích giúp bạn dự đoán chính xác các sự kiện trong khoảng thời gian cụ thể.

Chúc các bạn áp dụng thành công và đạt được kết quả tốt nhất!