Phương pháp xác định phương trình đường thẳng
22/02/2025
Nội dung bài viết
Để xác định phương trình đường thẳng, bạn cần hai yếu tố chính: a) một điểm thuộc đường thẳng; và b) hệ số góc (hay độ dốc) của đường thẳng đó. Tùy vào từng trường hợp, cách tìm kiếm và xử lý thông tin này có thể khác nhau. Bài viết này tập trung vào dạng phương trình hệ số góc và tung độ gốc y = mx + b, thay vì dạng hệ số góc và một điểm cụ thể (y - y1) = m(x - x1).
Các bước thực hiện
Thông tin tổng quan
Xác định hệ số góc và một điểm thuộc đường thẳng
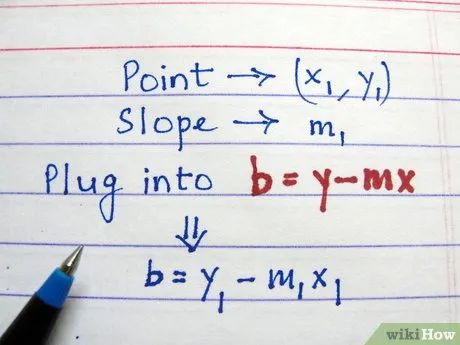
Xác định tung độ gốc trong phương trình của bạn. Tung độ gốc (biến b trong phương trình) là điểm mà đường thẳng cắt trục tung. Bạn có thể tính toán tung độ gốc bằng cách sắp xếp lại phương trình để tìm b. Công thức mới sẽ là: b = y - mx.
- Thay thế hệ số góc và tọa độ vào công thức trên.
- Nhân hệ số góc (m) với hoành độ của điểm đã cho.
- Lấy tung độ của điểm TRỪ ĐI kết quả vừa tính.
- Bạn đã tìm ra b, tung độ gốc của phương trình.
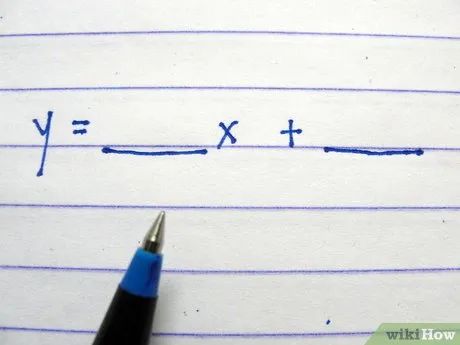
Viết công thức: y = ____ x + ____ , để trống các khoảng trắng.
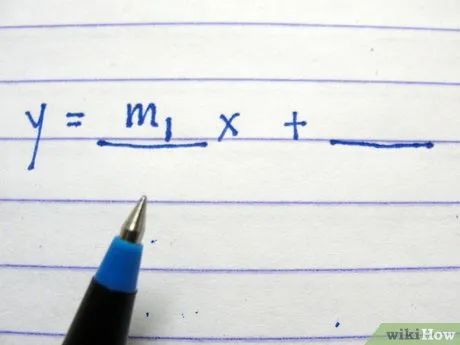
Điền hệ số góc vào khoảng trắng đầu tiên, đứng trước x.
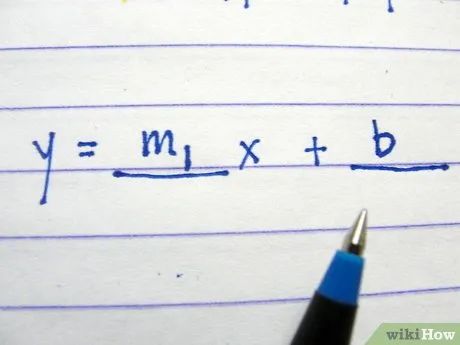
Điền tung độ gốc vào khoảng trắng thứ hai mà bạn đã tính toán.
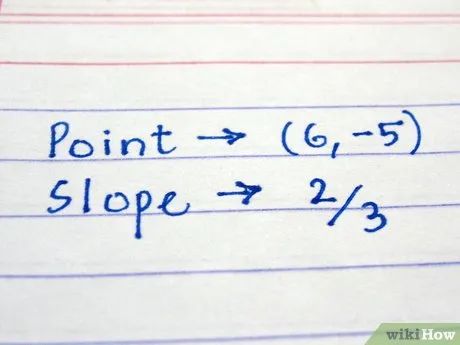
Giải bài toán mẫu. "Tìm phương trình đường thẳng đi qua điểm (6, -5) với hệ số góc là 2/3."
- Sắp xếp lại phương trình: b = y - mx.
- Thay giá trị và tính toán:
- b = -5 - (2/3)6.
- b = -5 - 4.
- b = -9
- Kiểm tra lại xem tung độ gốc có đúng là -9 không.
- Viết phương trình: y = 2/3 x - 9
Xác định hai điểm thuộc đường thẳng
Tính hệ số góc giữa hai điểm. Hệ số góc, hay "độ dốc", thể hiện sự thay đổi của đường thẳng khi di chuyển ngang một đơn vị. Công thức tính hệ số góc là: (Y2 - Y1) / (X2 - X1).
- Thay tọa độ hai điểm vào công thức (hai giá trị y và hai giá trị x). Thứ tự thay thế không quan trọng, miễn là bạn nhất quán. Ví dụ:
- Điểm (3, 8) và (7, 12): (12 - 8) / (7 - 3) = 4/4 = 1.
- Điểm (5, 5) và (9, 2): (2 - 5) / (9 - 5) = -3/4.
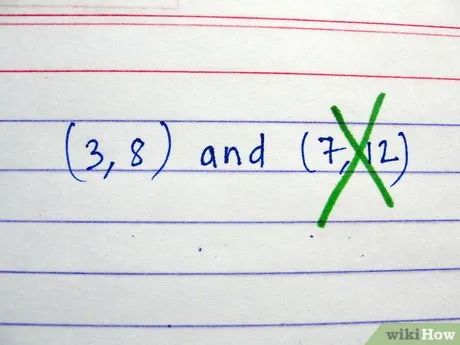
Chọn một cặp tọa độ để tiếp tục bài toán. Loại bỏ hoặc che đi cặp tọa độ còn lại để tránh nhầm lẫn.
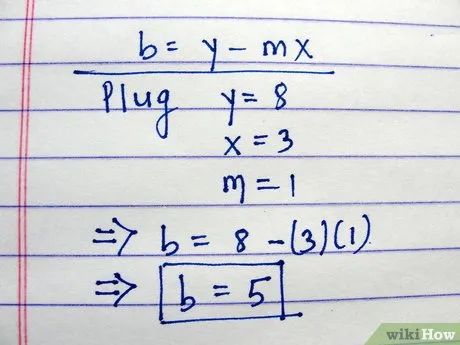
Tính tung độ gốc của phương trình. Sắp xếp lại công thức y = mx + b thành b = y - mx.
- Thay hệ số góc và tọa độ vào công thức.
- Nhân hệ số góc (m) với hoành độ của điểm.
- Lấy tung độ của điểm TRỪ ĐI kết quả vừa tính.
- Bạn đã tìm được b, tung độ gốc.
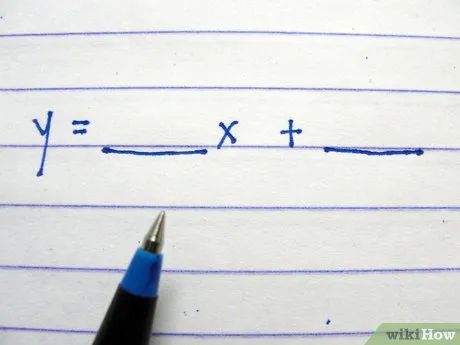
Viết công thức: y = ____ x + ____ , để trống các khoảng trắng.
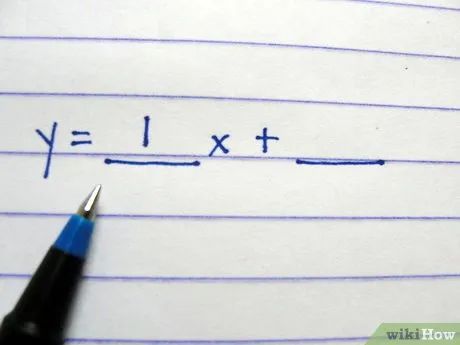
Điền hệ số góc vào khoảng trắng đầu tiên, đứng trước x.
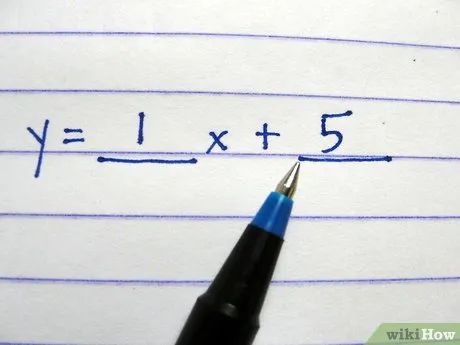
Điền tung độ gốc vào khoảng trắng thứ hai.
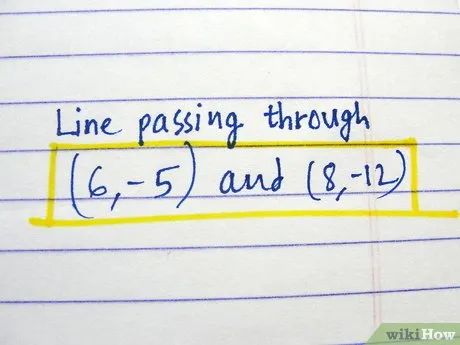
Giải bài toán mẫu. "Cho hai điểm (6, -5) và (8, -12). Tìm phương trình đường thẳng đi qua hai điểm trên."
- Tìm hệ số góc: (Y2 - Y1) / (X2 - X1).
- (-12 - (-5)) / (8 - 6) = -7 / 2.
- Hệ số góc là -7/2 (đường thẳng đi xuống 7 đơn vị và sang phải 2 đơn vị).
- Sắp xếp lại phương trình: b = y - mx.
- Thay số và tính toán:
- b = -12 - (-7/2)8.
- b = -12 - (-28).
- b = -12 + 28.
- b = 16.
- Lưu ý: Khi thay tọa độ, nếu dùng 8, bạn phải dùng -12. Nếu dùng 6, bạn phải dùng -5.
- Kiểm tra lại để đảm bảo tung độ gốc là 16.
- Viết phương trình: y = -7/2 x + 16.
Xác định một điểm và một đường thẳng song song
Xác định hệ số góc của đường thẳng song song. Hệ số góc là hệ số của x khi y đứng một mình.
- Trong y = 3/4 x + 7, hệ số góc là 3/4.
- Trong y = 3x - 2, hệ số góc là 3.
- Trong y = 3x, hệ số góc là 3.
- Trong y = 7, hệ số góc là 0 (không có x).
- Trong y = x - 7, hệ số góc là 1.
- Trong -3x + 4y = 8, hệ số góc là 3/4.
- Để tìm hệ số góc, sắp xếp lại phương trình: 4y = 3x + 8.
- Chia cả hai vế cho 4: y = 3/4x + 2.
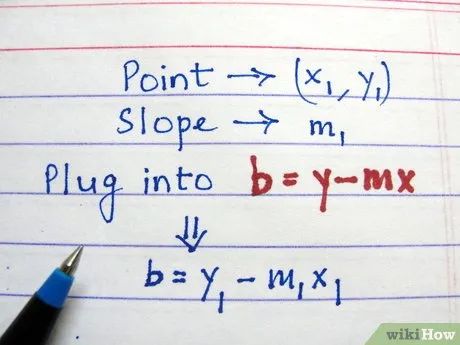
Tính tung độ gốc bằng cách sử dụng hệ số góc đã tìm và công thức b = y - mx.
- Thay hệ số góc và tọa độ vào công thức.
- Nhân hệ số góc (m) với hoành độ của điểm.
- Lấy tung độ của điểm TRỪ ĐI kết quả vừa tính.
- Bạn đã tìm được b, tung độ gốc.
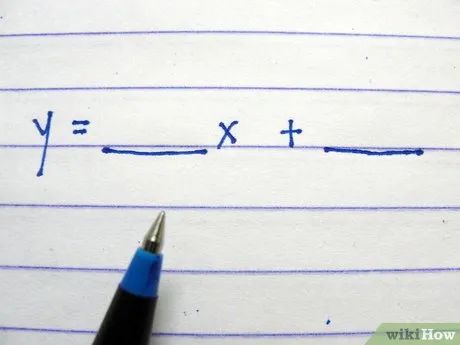
Viết công thức: y = ____ x + ____ , để trống các khoảng trắng.
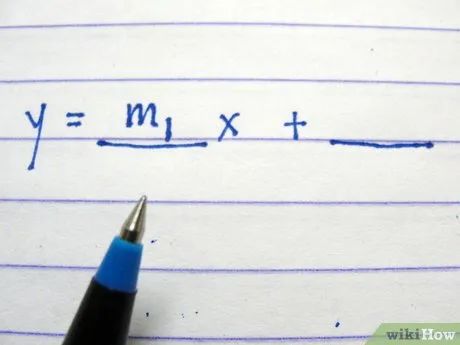
Điền hệ số góc đã tìm vào khoảng trắng đầu tiên, đứng trước x. Các đường thẳng song song có cùng hệ số góc, vì vậy hệ số góc của chúng luôn giống nhau.
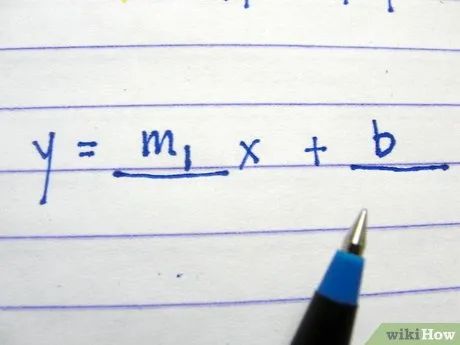
Điền tung độ gốc vào khoảng trắng thứ hai.
Xác định một điểm và một đường thẳng vuông góc
Xác định hệ số góc của đường thẳng đã cho. Tham khảo các ví dụ trước để hiểu rõ hơn.
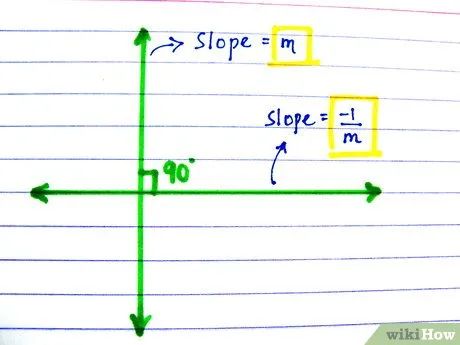
Tìm nghịch đảo trái dấu của hệ số góc đó. Đảo ngược giá trị và đổi dấu. Hai đường thẳng vuông góc có hệ số góc nghịch đảo trái dấu. Ví dụ:
- 2/3 trở thành -3/2.
- -6/5 trở thành 5/6.
- 3 (hoặc 3/1) trở thành -1/3.
- -1/2 trở thành 2.
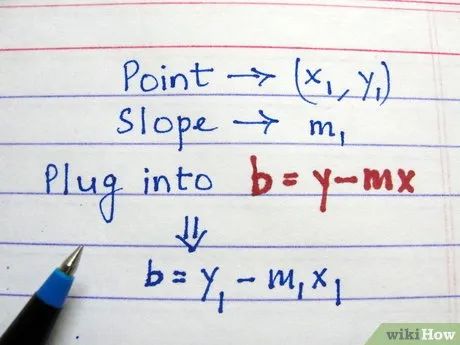
Tính tung độ gốc bằng hệ số góc ở bước 2 và công thức b = y - mx.
- Thay hệ số góc và tọa độ vào công thức.
- Nhân hệ số góc (m) với hoành độ của điểm.
- Lấy tung độ của điểm TRỪ ĐI kết quả vừa tính.
- Bạn đã tìm được b, tung độ gốc.
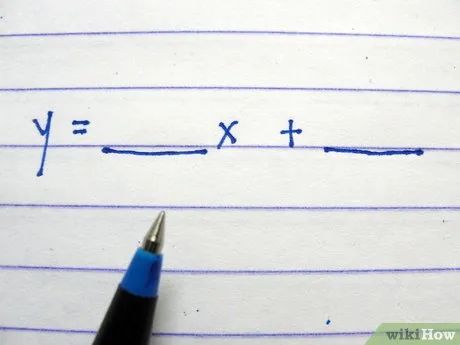
Viết công thức: y = ____ x + ____ , để trống các khoảng trắng.
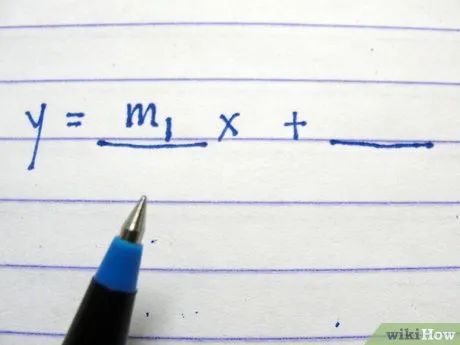
Điền hệ số góc tính được ở bước 2 vào khoảng trắng đầu tiên, đứng trước x.
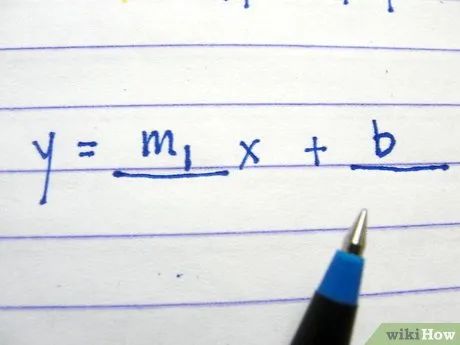
Điền tung độ gốc vào khoảng trắng thứ hai.
Du lịch
Ẩm thực
Khám phá
Đi Phượt
Vẻ đẹp Việt Nam
Chuyến đi
Có thể bạn quan tâm

Tải FF Advance OB42 APK chính thức cho Android từ ff-advance.ff.garena.com

7 Địa điểm vàng cho những tín đồ kính mắt tại TP. Pleiku, Gia Lai

Top 7 loại băng vệ sinh tampon chất lượng hàng đầu dành cho phái đẹp

8 Bí quyết vàng giúp bạn tự tin chinh phục buổi phỏng vấn ngân hàng

Top 6 Xưởng/Gara sửa chữa ô tô uy tín, chất lượng hàng đầu tại quận Long Biên, Hà Nội


