Công thức tính đường cao trong tam giác vuông cân & Ví dụ minh họa chi tiết

Mỗi loại tam giác đều có cách tính đường cao riêng biệt. Bạn có biết công thức tính đường cao trong tam giác vuông cân là gì không? Cùng Tripi khám phá công thức và các ví dụ cụ thể trong bài viết dưới đây.

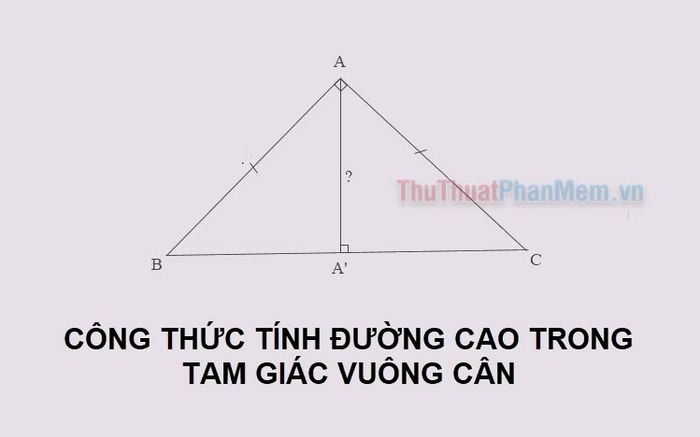
1. Khái niệm đường cao trong tam giác vuông cân

Tam giác vuông cân là tam giác đặc biệt với một góc vuông và hai cạnh góc vuông bằng nhau. Cạnh huyền là cạnh đối diện góc vuông, hai góc còn lại bằng 45 độ.

Trong tam giác vuông cân, đường cao là đoạn thẳng kẻ từ đỉnh góc vuông, vuông góc với cạnh huyền, đồng thời chia cạnh huyền thành hai phần bằng nhau một cách cân đối.

2. Đặc điểm nổi bật của đường cao trong tam giác vuông cân

Đường cao trong tam giác vuông cân mang những tính chất đặc trưng sau:

• Đường cao đóng vai trò là đường phân giác của góc vuông: Giao điểm của đường cao với cạnh huyền chính là trung điểm, nằm trên đường phân giác chia góc vuông thành hai góc 45 độ.
• Đường cao cũng là đường trung bình của tam giác: Nó đi qua trung điểm của cạnh góc vuông và cạnh huyền, tạo sự cân bằng hoàn hảo.
• Đường cao chia tam giác vuông cân thành hai tam giác vuông nhỏ bằng nhau: Hai tam giác này có cạnh huyền chung là đường cao và các cạnh góc vuông tương ứng bằng nhau.
• Đường cao còn là đường tâm của tam giác: Giao điểm của các đường cao chính là tâm của tam giác vuông cân.

3. Công thức tính đường cao trong tam giác vuông cân và ví dụ minh họa

Xét tam giác ABC vuông cân tại A, đường cao từ đỉnh A được ký hiệu là AA’.

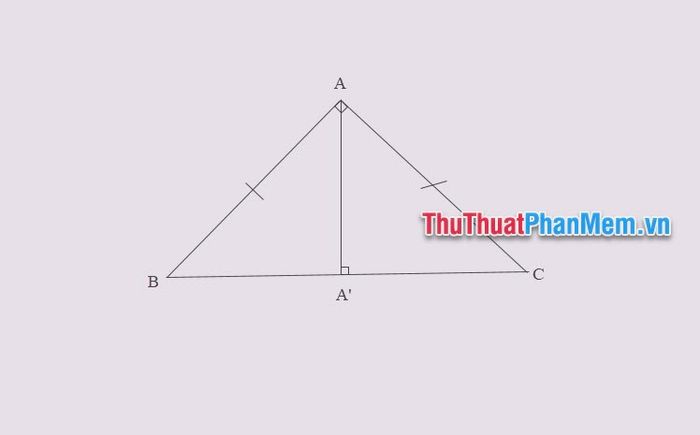
Ta có các thông tin sau:

• Đường cao từ đỉnh B chính là đoạn thẳng BA.
• Đường cao từ đỉnh C chính là đoạn thẳng CA.
• Mục tiêu của chúng ta là xác định độ dài đường cao AA’ từ đỉnh A.

Xét tam giác vuông AA’B, ta có: ˆABA′=45∘$\widehat{AB{A}^{\prime }}={45}^{\circ }$ vì tam giác ABC vuông cân tại A.

Theo tính chất đường cao trong tam giác vuông cân, đường cao AA’ chia góc vuông ˆBAC$\widehat{BAC}$ thành hai góc bằng nhau, mỗi góc 45 độ.

Suy ra, tam giác AA’B vuông cân tại A’.

Do đó, AA′=BA′=12BC$A{A}^{\prime }=B{A}^{\prime }=\frac{1}{2}BC$

Như vậy, chiều cao từ đỉnh góc vuông xuống cạnh huyền trong tam giác vuông cân có độ dài bằng một nửa độ dài cạnh huyền.

Ví dụ 1: Cho tam giác ABC vuông cân tại A, cạnh huyền BC = 6cm. Hãy tính chiều cao AA′$A{A}^{\prime }$ của tam giác.

Lời giải chi tiết:

Vì tam giác ABC vuông cân tại A, nên ta có công thức: AA′=12BC$A{A}^{\prime }=\frac{1}{2}BC$

Vậy AA′=12×6=3 cm$A{A}^{\prime }=\frac{1}{2}\times 6=3cm$

Ví dụ 2: Cho tam giác vuông cân ABC với hai cạnh góc vuông AB = AC = 3cm. Hãy tính độ dài đường cao AH.

Lời giải chi tiết:

Áp dụng định lý Pytago trong tam giác vuông ABC, ta có:

BC=√AB2+AC2=√32+32=√18=3√2 cm$BC=\sqrt{A{B}^2+A{C}^2}=\sqrt{3^2+3^2}=\sqrt{18}=3\sqrt{2}cm$

Vậy độ dài đường cao AH=12BC=123√2=32√2 cm$AH=\frac{1}{2}BC=\frac{1}{2}3\sqrt{2}=\frac{3}{2}\sqrt{2}cm$

Như vậy, bạn đã cùng Tripi khám phá về đường cao trong tam giác vuông cân, những tính chất đặc biệt của nó, cũng như công thức tính toán và ví dụ minh họa cụ thể. Hy vọng bài viết đã mang đến những kiến thức bổ ích, giúp bạn ứng dụng hiệu quả trong học tập. Cảm ơn bạn đã theo dõi và ủng hộ!