Công thức tính đường chéo hình thoi kèm ví dụ minh họa chi tiết

Bạn đang tìm kiếm công thức tính đường chéo hình thoi? Hình thoi, cũng như các hình học khác, đều có những công thức tính toán riêng biệt. Bên cạnh việc tính diện tích và chu vi, tính đường chéo hình thoi là một dạng toán thú vị và thường xuyên xuất hiện trong chương trình học. Cùng Tripi khám phá công thức và các ví dụ minh họa cụ thể trong bài viết dưới đây.

I. Hình thoi là gì? Đường chéo hình thoi được hiểu như thế nào?

Hình thoi trong hình học Euclide là một tứ giác đặc biệt với bốn cạnh có độ dài bằng nhau. Nó cũng được xem là hình bình hành với hai cạnh kề bằng nhau hoặc hình bình hành có hai đường chéo vuông góc với nhau.

Tính chất đặc trưng của hình thoi

• Các góc đối diện luôn bằng nhau
• Hai đường chéo vuông góc và cắt nhau tại trung điểm của mỗi đường
• Hai đường chéo đồng thời là đường phân giác của các góc trong hình thoi
• Hình thoi sở hữu mọi tính chất của hình bình hành, bao gồm cạnh đối song song và bằng nhau, góc đối bằng nhau, và hai đường chéo cắt nhau tại trung điểm

Đường chéo hình thoi là đoạn thẳng nối hai đỉnh đối diện, chia hình thoi thành hai tam giác đều với các cạnh tương ứng bằng nhau. Mỗi hình thoi có hai đường chéo, chúng giao nhau tại trung điểm và tạo thành các góc vuông.

II. Công thức tính đường chéo hình thoi một cách chính xác

1. Công thức tính đường chéo hình thoi dựa trên diện tích

Công thức tính diện tích hình thoi được biểu diễn như sau: S=d1×d22$S=\frac{d_1\times d_2}{2}$

Trong đó: S là diện tích hình thoi; d1 và d2$d_1\text{ và }{d}_2$ là hai đường chéo của hình thoi.

Từ công thức trên, ta suy ra cách tính đường chéo hình thoi: d1=S×2d2$d_1=\frac{S\times 2}{d_2}$ hoặc d2=S×2d1$d_2=\frac{S\times 2}{d_1}$

2. Công thức tính đường chéo hình thoi dựa trên định lý cosin

Định lý cosin thể hiện mối quan hệ giữa độ dài các cạnh của một tam giác và cosin của góc tương ứng.

Công thức cosin được biểu diễn như sau: c2=a2+b2+2abcosγ$c^2=a^2+b^2+2ab\cos \gamma$

Trong đó: a, b, c là độ dài các cạnh của tam giác, và γ là góc nằm giữa hai cạnh a và b.

3. Công thức tính đường chéo hình thoi dựa trên định lý Pytago

Áp dụng định lý Pytago vào tam giác vuông được tạo bởi giao điểm của hai đường chéo hình thoi, ta có bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông.

Ví dụ 1: Xét hình thoi ABCD với độ dài cạnh a và góc ABC = 60 độ. Hãy tính độ dài hai đường chéo của hình thoi.

Lời giải chi tiết

Do hình thoi có các cạnh bằng nhau, nên hình thoi ABCD có tất cả các cạnh đều bằng a.

Xét tam giác ABC trong hình thoi ABCD, ta có: AB = BC = a.

Góc ABC được cho là 60 độ.

Từ đó suy ra, tam giác ABC là một tam giác đều với độ dài các cạnh bằng a.

Do đó, AB = AC = BC = a. Đường chéo chính AC có độ dài bằng a.

Gọi I là giao điểm của hai đường chéo. Áp dụng định lý Pytago cho tam giác vuông ABI, ta có:

BI2=AB2−AI2=a2−(a2)2=a2(1−14)=34a2$B{I}^2=A{B}^2-A{I}^2=a^2-{\left(\frac{a}{2}\right)}^2=a^2\left(1-\frac{1}{4}\right)=\frac{3}{4}{a}^2$

Suy ra: BI=a√32$BI=\frac{a\sqrt{3}}{2}$

Do đó, đường chéo BD = BI x 2 = a√3$a\sqrt{3}$

III. Các ví dụ minh họa chi tiết

Dạng 1: Bài toán cho biết độ dài một đường chéo và yêu cầu tìm độ dài đường chéo còn lại

Ví dụ 2: Cho hình thoi có đường chéo nhỏ dài 4 cm, đường chéo lớn gấp đôi đường chéo nhỏ. Hãy tính độ dài đường chéo lớn của hình thoi.

Lời giải chi tiết

Gọi đường chéo nhỏ và đường chéo lớn của hình thoi lần lượt là d1$d_1$ và d2$d_2$.

Theo đề bài, ta có: d1$d_1$ = 4 cm và d2$d_2$ = 2 x d1$d_1$.

Vậy độ dài đường chéo lớn d2$d_2$ = 4 x 2 = 8 cm.

Ví dụ 3: Cho hình thoi có hiệu độ dài hai đường chéo là 10 cm, trong đó đường chéo thứ nhất gấp 3 lần đường chéo thứ hai. Hãy tính độ dài của hai đường chéo này.

Lời giải chi tiết

Gọi đường chéo lớn và đường chéo nhỏ của hình thoi lần lượt là d1$d_1$ và d2$d_2$.

Theo đề bài, ta có: d1$d_1$ - d2$d_2$ = 10 cm và d1$d_1$ = 3 x d2$d_2$.

Từ đó suy ra: 3d2$d_2$ - d2$d_2$ = 10, suy ra d2$d_2$ = 5 cm và d1$d_1$ = 15 cm.

Dạng 2: Bài toán cho biết diện tích và độ dài một đường chéo

Với dạng bài này, bạn chỉ cần áp dụng công thức tính đường chéo hình thoi dựa trên diện tích đã được trình bày ở phần trên.

Ví dụ 4: Cho hình thoi có diện tích 200 cm² và độ dài một đường chéo là 10 cm. Hãy tính độ dài đường chéo còn lại.

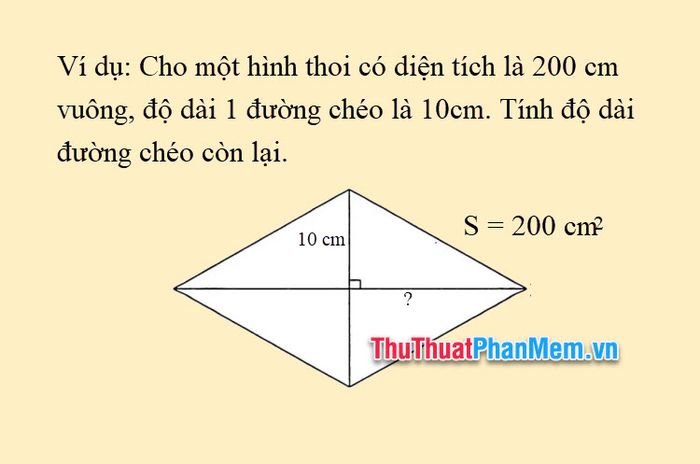
Lời giải:

Áp dụng công thức tính đường chéo hình thoi dựa trên diện tích: d1=s×2d2$d1=\frac{s\times 2}{d2}$, ta có:

Độ dài đường chéo còn lại được tính bằng: (200 x 2) : 10 = 40 cm.

Vậy, đường chéo còn lại của hình thoi có độ dài là 40 cm.

Dạng 3: Bài toán cho biết độ dài cạnh và đường cao của hình thoi, yêu cầu tìm độ dài hai đường chéo

Ví dụ 5: Cho hình thoi ABCD có cạnh dài 12,5 cm, đường cao 6,72 cm và đường chéo AC ngắn hơn BD. Hãy tính độ dài hai đường chéo AC và BD.

Lời giải chi tiết

Áp dụng công thức tính diện tích hình thoi: S = h x a = 6,72 x 12,5 = 84 cm².

=>AC×BD2$=>\frac{AC\times BD}{2}$ = 84, suy ra 2AC x BD = 336

Gọi O là giao điểm của hai đường chéo trong hình thoi.

Xét tam giác vuông AOB, ta có: AB2=OA2+OB2$A{B}^2=O{A}^2+O{B}^2$

Với OA=12AC;OB=12BD=>12,52=(AC2+BD2)4<=>625=AC2+BD2$OA=\frac{1}{2}AC;OB=\frac{1}{2}BD=>12,5^2=\frac{(A{C}^2+B{D}^2)}{4}<=>625=A{C}^2+B{D}^2$

Từ đó suy ra: AC + BD = 31 (1).

AC² + BD² = 625, tương đương với AC² + BD² - AC x BD = 625 - 336, hay (BD - AC)² = 289.

Suy ra: BD – AC = 17 (vì BD > AC theo đề bài) (2).

Kết hợp (1) và (2), ta được: BD = 24 cm và AC = 7 cm.

Tripi đã tổng hợp và chia sẻ những kiến thức cơ bản về hình thoi, bao gồm công thức tính đường chéo dựa trên diện tích, định lý cosin, định lý Pytago cùng các ví dụ minh họa chi tiết. Hy vọng bài viết này sẽ giúp bạn nắm vững cách tính đường chéo hình thoi và tự tin giải quyết các bài toán liên quan. Cảm ơn bạn đã dành thời gian theo dõi và ủng hộ bài viết.