Phương pháp tính đường chéo hình vuông và hình chữ nhật

Bạn đang cần tính đường chéo hình vuông hoặc hình chữ nhật nhưng chưa nhớ rõ cách làm? Hãy cùng khám phá lại công thức qua bài viết dưới đây để nắm vững kiến thức này nhé.

Bài viết này sẽ hướng dẫn chi tiết cách tính đường chéo hình vuông và hình chữ nhật, mời bạn đọc cùng theo dõi.

Công thức tính đường chéo hình vuông

Trong hình học Euclid, hình vuông được định nghĩa là một tứ giác đều. Nó có thể được xem như một hình chữ nhật với các cạnh bằng nhau hoặc một hình thoi với hai đường chéo có độ dài bằng nhau.

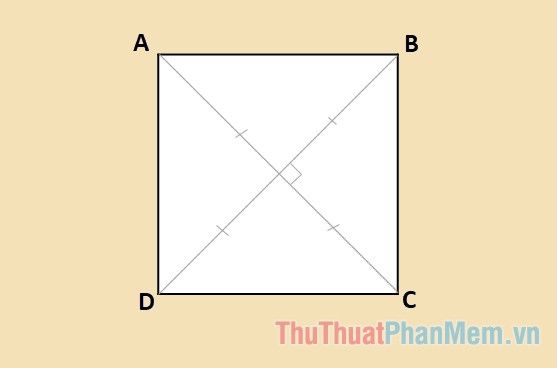
Đặc điểm nổi bật của hình vuông

• Hai đường chéo của hình vuông không chỉ bằng nhau mà còn vuông góc và cắt nhau tại trung điểm của mỗi đường.
• Hình vuông có cả đường tròn nội tiếp và ngoại tiếp, với tâm của cả hai trùng nhau tại giao điểm của hai đường chéo.
• Mỗi đường chéo chia hình vuông thành hai phần có diện tích bằng nhau.
• Điểm giao nhau của các đường phân giác, trung tuyến, và trung trực đều nằm tại một điểm duy nhất.
• Hình vuông kế thừa tất cả các tính chất của hình chữ nhật, hình bình hành, và hình thoi.

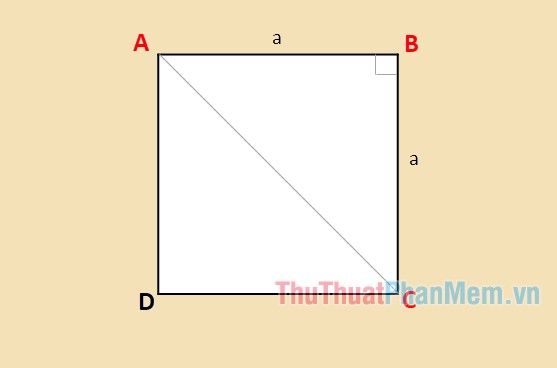
Phương pháp tính đường chéo hình vuông

Theo tính chất của hình vuông, hai đường chéo của nó không chỉ bằng nhau mà còn chia hình vuông thành hai tam giác vuông cân có diện tích bằng nhau. Đường chéo hình vuông chính là cạnh huyền của hai tam giác này. Do đó, để tính đường chéo, bạn chỉ cần áp dụng định lý Pytago cho tam giác vuông.

Giả sử bạn có hình vuông ABCD với độ dài cạnh là a. Đường chéo AC chia hình vuông thành hai tam giác vuông cân ABC và ACD. Áp dụng định lý Pytago cho tam giác vuông cân ABC, ta có:

AC2=AB2+BC2$A{C}^2=A{B}^2+B{C}^2$

HayAC2=a2+a2=2a2$HayA{C}^2=a^2+a^2=2a^2$

⇒AC=a√2$\Rightarrow AC=a\sqrt{2}$

Như vậy, đường chéo của hình vuông có cạnh độ dài a được tính bằng công thức a√2$a\sqrt{2}$.

Phương pháp tính đường chéo hình chữ nhật

Trong hình học Euclid, hình chữ nhật là một tứ giác lồi với bốn góc vuông. Đây cũng là một dạng hình bình hành đặc biệt với hai đường chéo có độ dài bằng nhau.

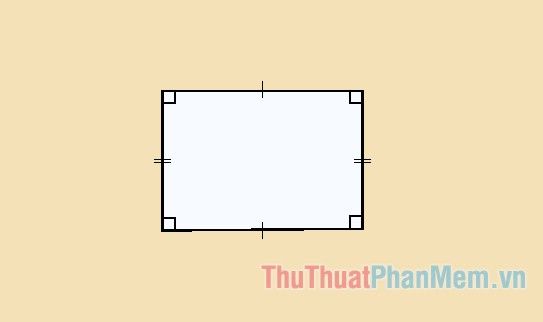
Đặc điểm nổi bật của hình chữ nhật

• Hai đường chéo của hình chữ nhật không chỉ bằng nhau mà còn cắt nhau tại trung điểm của mỗi đường.
• Hình chữ nhật sở hữu tất cả các tính chất của hình thang cân và hình bình hành.
• Các đường chéo trong hình chữ nhật cắt nhau tạo thành bốn tam giác cân.

Phương pháp tính đường chéo hình chữ nhật

Hình chữ nhật có bốn góc vuông và hai đường chéo bằng nhau. Một đường chéo sẽ chia hình chữ nhật thành hai tam giác vuông, trong đó đường chéo đóng vai trò là cạnh huyền, còn hai cạnh của hình chữ nhật là hai cạnh góc vuông. Để tính đường chéo, bạn có thể áp dụng định lý Pytago một cách dễ dàng.

Giả sử bạn có hình chữ nhật ABCD với chiều dài là a và chiều rộng là b, đường chéo AC được biểu diễn như hình vẽ dưới đây.

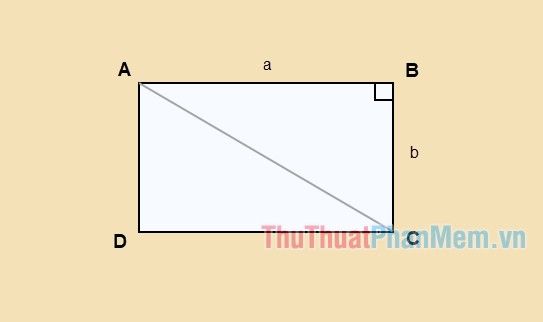
Áp dụng định lý Pytago cho tam giác vuông ABC, ta có:

AC2=AB2+BC2$A{C}^2=A{B}^2+B{C}^2$

⇔AC2=a2+b2$\iff A{C}^2=a^2+b^2$

⇔AC=√(a2+b2)$\iff AC=\sqrt{\left(a^2+b^2\right)}$

Như vậy, đường chéo của hình chữ nhật với chiều dài a và chiều rộng b được tính bằng công thức √(a2+b2)$\sqrt{\left(a^2+b^2\right)}$.

Bài viết trên đã chia sẻ cách tính đường chéo hình vuông và hình chữ nhật một cách chi tiết. Dù là hình vuông hay hình chữ nhật, bạn chỉ cần áp dụng định lý Pytago để tính toán đường chéo một cách dễ dàng. Chúc các bạn áp dụng thành công!