Tổng hợp đầy đủ các hàm kỹ thuật hữu ích trong Excel

Bài viết dưới đây mang đến cái nhìn chi tiết và toàn diện về các hàm kỹ thuật trong Excel, giúp bạn áp dụng hiệu quả vào công việc.

1. Hàm CONVERT

Mô tả: Hàm hỗ trợ chuyển đổi linh hoạt giữa các đơn vị đo lường như trọng lượng, khối lượng, độ dài, thời gian, năng lượng và nhiều hơn nữa.

Cú pháp: CONVERT(number, from_unit, to_unit).

Trong đó:

- number: giá trị cần được chuyển đổi.

- from_unit: Đơn vị đo lường gốc của giá trị cần chuyển đổi.

- to_unit: Đơn vị đo lường đích mà bạn muốn chuyển đổi giá trị tới.

Ví dụ: CONVERT(5, "g", "ozm"): Chuyển đổi 5 gram sang đơn vị ounce khối lượng.

Quy tắc viết đơn vị chuyển đổi:

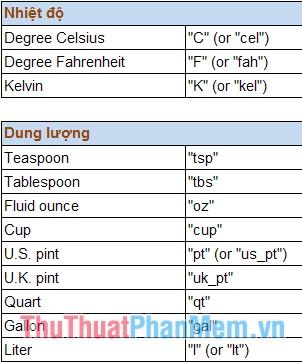
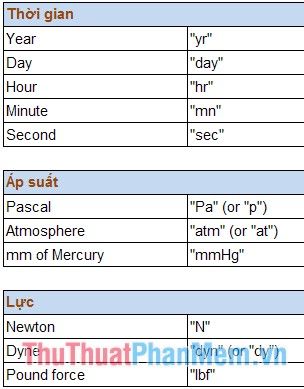
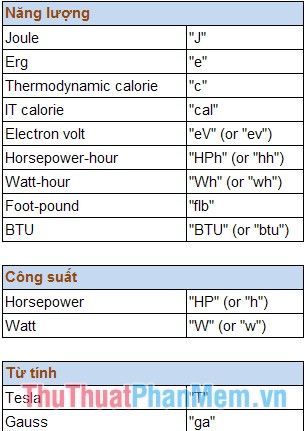
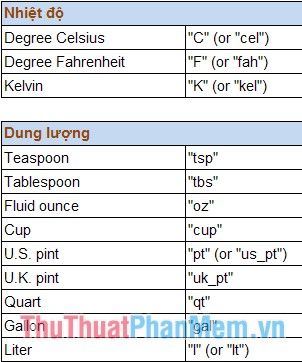
2. Hàm BESSELI

Mô tả: Hàm trả về giá trị của hàm BESSELI In(x), một hàm biến đổi quan trọng trong toán học và kỹ thuật.

Cú pháp: BESSELI(x, n).

Trong đó:

- x là giá trị đầu vào để tính toán hàm BESSELI.

- n là bậc của hàm, nếu n là số thập phân, hàm sẽ tự động làm tròn giá trị của n.

Lưu ý:

- Nếu n < 0, hàm sẽ trả về lỗi #NUM!.

- x và n phải là giá trị số, nếu nhập sai định dạng, hàm sẽ báo lỗi #VALUE.

Ví dụ: BESSELI(2.5, 3) => Hàm BESSELI biến đổi In(x) bậc 1 tại giá trị 1.5 cho kết quả là 0.47437.

3. Hàm BESSELJ

Mô tả: Hàm trả về giá trị của hàm BESSELJ Jn(x), một hàm biến đổi quan trọng trong toán học và kỹ thuật.

Cú pháp: BESSELJ(x, n).

Trong đó:

- x là giá trị đầu vào để tính toán hàm BESSELJ.

- n là bậc của hàm, nếu n là số thập phân, hàm sẽ tự động làm tròn giá trị của n.

Lưu ý:

- Nếu n < 0, hàm sẽ trả về lỗi #NUM!.

- x và n phải là giá trị số, nếu nhập sai định dạng, hàm sẽ báo lỗi #VALUE.

Ví dụ: BESSELJ(2.5, 3) => Hàm BESSELJ biến đổi Jn(x) bậc 1 tại giá trị 1.5 cho kết quả là 0.2166.

4. Hàm BESSELK

Mô tả: Hàm trả về giá trị của hàm BESSELK Kn(x), một hàm biến đổi quan trọng trong toán học và kỹ thuật.

Cú pháp: BESSELK(x, n).

Trong đó:

- x là giá trị đầu vào để tính toán hàm BESSELK.

- n là bậc của hàm, nếu n là số thập phân, hàm sẽ tự động làm tròn giá trị của n.

Lưu ý:

- Nếu n < 0, hàm sẽ trả về lỗi #NUM!.

- x và n phải là giá trị số, nếu nhập sai định dạng, hàm sẽ báo lỗi #VALUE.

Ví dụ: BESSELK(2.5, 3) => Hàm BESSELK biến đổi Kn(x) bậc 1 tại giá trị 1.5 cho kết quả là 0.268227.

5. Hàm BESSELY

Mô tả: Hàm trả về giá trị của hàm BESSELY Yn(x), một hàm biến đổi quan trọng trong toán học và kỹ thuật.

Cú pháp: BESSELY(x, n).

Trong đó:

- x là giá trị đầu vào để tính toán hàm BESSELY.

- n là bậc của hàm, nếu n là số thập phân, hàm sẽ tự động làm tròn giá trị của n.

Lưu ý:

- Nếu n < 0, hàm sẽ trả về lỗi #NUM!.

- x và n phải là giá trị số, nếu nhập sai định dạng, hàm sẽ báo lỗi #VALUE.

Ví dụ: BESSELY(2.5, 3) => Hàm BESSELY biến đổi Yn(x) bậc 1 tại giá trị 1.5 cho kết quả là -0.75605.

6. Hàm BIN2DEC

Mô tả: Hàm chuyển đổi giá trị nhị phân thành giá trị thập phân một cách chính xác và hiệu quả.

Cú pháp: BIN2DEC(number).

Trong đó:

number là giá trị nhị phân cần được chuyển đổi sang hệ thập phân.

Lưu ý: Nếu number vượt quá 10 ký tự, hàm sẽ trả về lỗi #NUM!.

7. Hàm DEC2BIN

Mô tả: Hàm chuyển đổi giá trị thập phân sang hệ nhị phân một cách chính xác và linh hoạt.

Cú pháp: DEC2BIN(number [, places]).

Trong đó:

- number là giá trị thập phân cần chuyển đổi, places là tham số tùy chọn.

- places là số lượng ký tự mong muốn trong kết quả trả về.

8. Hàm BIN2HEX

Mô tả: Hàm chuyển đổi giá trị nhị phân sang hệ thập lục phân một cách chính xác và hiệu quả.

Cú pháp: BIN2HEX(number [, places]).

Trong đó:

- number là giá trị nhị phân cần được chuyển đổi sang hệ thập lục phân.

- place (tham số tùy chọn): là số ký tự trong kết quả trả về. Nếu bỏ qua, Excel sẽ tự động chọn số ký tự tối thiểu để hiển thị kết quả.

Lưu ý:

- place phải là giá trị số tự nhiên và không âm.

- Nếu giá trị cần chuyển đổi vượt quá 10 ký tự, hàm sẽ trả về lỗi #NUM!.

- Nếu giá trị cần chuyển đổi là số âm, hàm sẽ bỏ qua tham số place và trả về kết quả gồm 10 ký tự trong hệ thập lục phân.

- Nếu kết quả trả về vượt quá số ký tự quy định trong place, hàm sẽ báo lỗi #NUM!.

- Nếu place là giá trị thập phân, Excel sẽ tự động lấy phần nguyên của place.

9. Hàm HEX2BIN

Mô tả: Hàm chuyển đổi giá trị từ hệ thập lục phân sang hệ nhị phân một cách chính xác và hiệu quả.

Cú pháp: HEX2BIN(number [, place]).

Trong đó:

- number là giá trị thập lục phân cần được chuyển đổi sang hệ nhị phân.

- place: tham số tùy chọn, quy định số ký tự trong kết quả trả về.

Lưu ý:

- Giá trị number cần được nhập trong dấu nháy kép, ví dụ: HEX2BIN("F").

10. Hàm BIN2OCT

Mô tả: Hàm chuyển đổi giá trị nhị phân sang hệ bát phân một cách chính xác và hiệu quả.

Cú pháp: BIN2OCT(number [, places]).

Trong đó: number là giá trị nhị phân cần chuyển đổi, places là tham số tùy chọn quy định số ký tự trong kết quả trả về.

Lưu ý: Các lưu ý tương tự như các hàm chuyển đổi hệ số khác.

11. Hàm OCT2BIN

Mô tả: Hàm chuyển đổi giá trị từ hệ bát phân sang hệ nhị phân một cách chính xác và hiệu quả.

Cú pháp: OCT2BIN(number [, places]).

Trong đó:

- number là giá trị bát phân cần được chuyển đổi sang hệ nhị phân.

- places: tham số tùy chọn, quy định số ký tự trong kết quả trả về. Nếu bỏ qua, Excel sẽ tự động chọn số ký tự tối thiểu để hiển thị kết quả.

Lưu ý: Các lưu ý tương tự như các hàm chuyển đổi hệ số khác.

12. Hàm COMPLEX

Mô tả: Hàm chuyển đổi hệ số thực và hệ số ảo thành số phức dưới dạng x + yi hoặc x + yj.

Cú pháp: COMPLEX(real_num, i_num [, suffix]).

Trong đó:

- real_num: hệ số thực, là một giá trị số.

- i_num: hệ số ảo, là một giá trị số.

- suffix: hậu tố của hệ số ảo trong số phức, mặc định là "i" nếu bỏ qua. Nếu khác, cần đặt trong dấu nháy kép.

Lưu ý: Nếu real_num hoặc i_num không phải là kiểu số, hàm sẽ trả về lỗi #VALUE. Hậu tố khác "i" hoặc "j" cũng sẽ gây lỗi #VALUE.

13. Hàm DEC2OCT

Mô tả: Hàm chuyển đổi giá trị thập phân sang hệ bát phân một cách chính xác và hiệu quả.

Cú pháp: DEC2OCT(number, places).

Trong đó:

- number: giá trị thập phân cần được chuyển đổi sang hệ bát phân.

- places: số ký tự trong kết quả trả về. Nếu nhập places, kết quả sẽ được thêm số 0 ở đầu nếu số ký tự nhỏ hơn places.

Lưu ý:

- Nếu number > 536.870.911 hoặc number < -536.870.912, hoặc places vượt quá 40 ký tự, hoặc places < 0, hàm sẽ trả về lỗi #NUM!.

- Nếu number hoặc places không phải là số, hàm sẽ trả về lỗi #VALUE!.

14. Hàm DELTA

Mô tả: Hàm kiểm tra xem hai giá trị có bằng nhau hay không, trả về 1 nếu bằng và 0 nếu khác.

Cú pháp: DELTA(number1, number2).

Trong đó:

- number1: giá trị thứ nhất cần so sánh.

- number2: giá trị thứ hai cần so sánh.

Nếu hai giá trị bằng nhau, hàm trả về 1; ngược lại, trả về 0 nếu chúng khác nhau.

Lưu ý: Cả hai giá trị phải là số, nếu nhập sai kiểu dữ liệu, hàm sẽ trả về lỗi #VALUE.

15. Hàm GESTEP

Mô tả: Hàm so sánh hai giá trị và kiểm tra xem giá trị đầu tiên có lớn hơn hoặc bằng giá trị thứ hai hay không.

Cú pháp: GESTEP(number, step).

Trong đó:

- number: giá trị cần được so sánh.

- step: giá trị ngưỡng để so sánh với number.

Nếu number >= step, hàm GESTEP trả về giá trị 1; ngược lại, trả về 0 nếu number < step.

Lưu ý:

- Nếu không nhập giá trị step, mặc định step = 0.

- Cả hai tham số của hàm phải là giá trị số, nếu không hàm sẽ trả về lỗi #VALUE.

16. Hàm IMAGINARY

Mô tả: Hàm trả về hệ số ảo của một số phức dưới dạng x + yi hoặc x + yj.

Cú pháp: IMAGINARY(number).

Trong đó:

- number là số phức cần trích xuất hệ số ảo.

17. Hàm IMDIV

Mô tả: Hàm tính toán thương của hai số phức, mang lại kết quả chính xác và hiệu quả.

Cú pháp: IMDIV(inumber1, inumber2).

Trong đó:

- inumber1 là số phức thứ nhất, đóng vai trò là số bị chia.

- inumber2 là số phức thứ hai, đóng vai trò là số chia.

18. Hàm IMLN

Mô tả: Hàm tính logarit tự nhiên của một số phức, mang lại kết quả chính xác và hữu ích.

Cú pháp: IMLN(inumber).

Trong đó:

- inumber là số phức cần tính toán logarit tự nhiên.

19. Hàm IMLOG2

Mô tả: Hàm tính logarit cơ số 2 của một số phức, mang lại kết quả chính xác và hữu ích.

Cú pháp: IMLOG2(inumber).

Trong đó:

- inumber là số phức cần tính toán logarit cơ số 2.

20. Hàm IMPRODUCT

Mô tả: Hàm tính toán tích của các số phức, mang lại kết quả chính xác và hiệu quả.

Cú pháp: IMPRODUCT(inumber1, inumber2, inumber3,…).

Trong đó:

- inumber là các số phức cần tính tích.

Lưu ý: Các số phức cần được nhập trong dấu nháy kép.

Ví dụ: IMPRODUCT("3-2i", "24-9i").

21. Hàm IMSIN

Mô tả: Hàm tính giá trị sin của một số phức, mang lại kết quả chính xác và hữu ích.

Cú pháp: IMSIN(number).

Trong đó:

- number là số phức cần tính toán giá trị sin.

22. Hàm IMSUB

Mô tả: Hàm tính hiệu của hai số phức, mang lại kết quả chính xác và hiệu quả.

Cú pháp: IMSUB(inumber1, inumber2).

Trong đó:

- inumber1 là số phức thứ nhất, đóng vai trò là số bị trừ.

- inumber2 là số phức thứ hai, đóng vai trò là số trừ.

23. Hàm IMABS

Mô tả: Hàm tính giá trị tuyệt đối của một số phức, mang lại kết quả chính xác và hữu ích.

Cú pháp: IMABS(inumber).

Trong đó:

- inumber là số phức cần tính toán giá trị tuyệt đối.

24. Hàm IMEXP

Mô tả: Hàm tính lũy thừa cơ số e của một số phức, mang lại kết quả chính xác và hữu ích.

Cú pháp: IMEXP(inumber).

Trong đó:

- inumber là số phức cần tính toán lũy thừa cơ số e.

25. Hàm IMCOS

Mô tả: Hàm tính giá trị cosin của một số phức, mang lại kết quả chính xác và hữu ích.

Cú pháp: IMCOS(inumber).

Trong đó:

- inumber là số phức cần tính toán giá trị cosin.

Lưu ý: Giá trị số phức cần được nhập trong dấu nháy kép.

26. Hàm IMLOG10

Mô tả: Hàm tính logarit cơ số 10 của một số phức, mang lại kết quả chính xác và hữu ích.

Cú pháp: IMLOG10(inumber).

Trong đó:

- inumber là số phức cần tính toán logarit cơ số 10.

27. Hàm IMPOWER

Mô tả: Hàm tính lũy thừa của một số phức, mang lại kết quả chính xác và hữu ích.

Cú pháp: IMPOWER(inumber, number).

Trong đó:

- inumber là số phức cần tính lũy thừa, number là số mũ.

28. Hàm IMREAL

Mô tả: Hàm trả về hệ số thực của một số phức, mang lại kết quả chính xác và hữu ích.

Cú pháp: IMREAL(inumber).

Trong đó:

- inumber là số phức cần trích xuất hệ số thực.

Lưu ý: Giá trị số phức cần được nhập trong dấu nháy kép.

Ví dụ: IMREAL("15-6i").

29. Hàm IMSQRT

Mô tả: Hàm tính căn bậc hai của một số phức, mang lại kết quả chính xác và hữu ích.

Cú pháp: IMSQRT(inumber).

Trong đó:

- inumber là số phức cần tính toán căn bậc hai.

30. Hàm IMSUM

Mô tả: Hàm tính tổng của các số phức, mang lại kết quả chính xác và hiệu quả.

Cú pháp: IMSUM(inumber1, inumber2, inumber3,…).

Trong đó:

- inumber là các số phức cần tính tổng, với tối đa 29 số phức.