Cách đánh giá ý nghĩa thống kê một cách chính xác

22/02/2025

Nội dung bài viết

Kiểm định giả thuyết thống kê dựa trên phân tích số liệu. Ý nghĩa thống kê được xác định thông qua giá trị p, thể hiện khả năng xảy ra của kết quả quan sát nếu giả thuyết không đúng. Nếu giá trị p nhỏ hơn ngưỡ ý nghĩa (thường là 0.05), bạn có thể bác bỏ giả thuyết không và chấp nhận giả thuyết nghịch. Sử dụng kiểm định t, bạn có thể tính toán giá trị p và xác định sự khác biệt giữa hai nhóm dữ liệu.

Các bước thực hiện

Thiết lập thực nghiệm của bạn

Xác định giả thuyết của bạn. Bước đầu tiên trong đánh giá ý nghĩa thống kê là xác định câu hỏi nghiên cứu và đưa ra giả thuyết. Giả thuyết là một tuyên bố về dữ liệu và sự khác biệt tiềm ẩn trong tổng thể. Mỗi thực nghiệm đều có giả thuyết không và giả thuyết nghịch. Thông thường, bạn sẽ so sánh hai nhóm để xem chúng có khác biệt hay không.

Giả thuyết không (H₀) khẳng định không có sự khác biệt giữa hai nhóm. Ví dụ: Sinh viên đọc tài liệu trước khi đến lớp không đạt điểm cao hơn.
Giả thuyết nghịch (H_a) phản bác giả thuyết không và là điều bạn muốn chứng minh. Ví dụ: Sinh viên đọc tài liệu trước khi đến lớp đạt điểm cao hơn.

Chọn mức ý nghĩa để xác định sự khác biệt có ý nghĩa trong dữ liệu. Mức ý nghĩa (alpha) là ngưỡng quyết định tính ý nghĩa của kết quả. Nếu giá trị p nhỏ hơn hoặc bằng alpha, dữ liệu được coi là có ý nghĩa thống kê.

Thông thường, mức ý nghĩa được đặt ở 0.05, tức là có 5% khả năng kết quả là ngẫu nhiên.
Mức tin cậy càng cao (giá trị p càng thấp), kết quả càng có ý nghĩa.
Để đạt độ tin cậy cao hơn, hãy giảm giá trị p xuống 0.01, thường được áp dụng trong kiểm soát chất lượng sản phẩm.
Đối với hầu hết các thí nghiệm, mức ý nghĩa 0.05 là phù hợp.

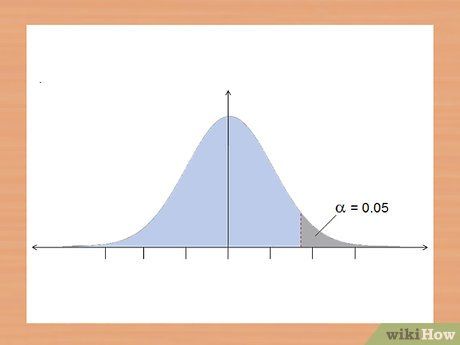
Quyết định sử dụng kiểm định một phía hay hai phía. Kiểm định t giả định dữ liệu tuân theo phân phối chuẩn, tạo thành đường cong hình chuông. Kiểm định t giúp xác định liệu dữ liệu có nằm ở phần đuôi của phân phối hay không.

Nếu không chắc chắn về hướng của dữ liệu, hãy sử dụng kiểm định hai phía để kiểm tra ý nghĩa ở cả hai hướng.
Nếu biết hướng kỳ vọng của dữ liệu, hãy dùng kiểm định một phía. Ví dụ, nếu bạn kỳ vọng điểm số sinh viên sẽ tăng, hãy chọn kiểm định một phía.

Xác định kích thước mẫu thông qua phân tích lực lượng. Lực lượng của kiểm định là khả năng phát hiện kết quả kỳ vọng với kích thước mẫu nhất định. Ngưỡng lực lượng phổ biến là 80%. Phân tích lực lượng đòi hỏi thông tin sơ bộ về giá trị trung bình và độ lệch chuẩn. Sử dụng công cụ trực tuyến để xác định kích thước mẫu tối ưu.

Nghiên cứu tiền đề nhỏ giúp thu thập dữ liệu cần thiết cho phân tích lực lượng.
Nếu không thể thực hiện nghiên cứu tiền đề, hãy tham khảo các nghiên cứu trước đó để ước tính giá trị trung bình và độ lệch chuẩn.

Tính toán độ lệch chuẩn

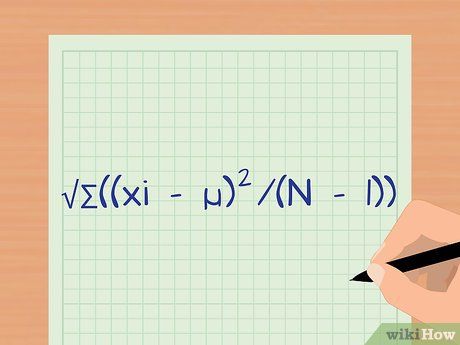
Hiểu công thức tính độ lệch chuẩn. Độ lệch chuẩn đo lường sự phân tán của dữ liệu, cho biết mức độ đồng nhất của các điểm dữ liệu. Công thức là s = √∑((x_i – µ)²/(N – 1)).

s là độ lệch chuẩn.
∑ biểu thị tổng của tất cả các quan sát.
x_i là từng giá trị dữ liệu.
µ là giá trị trung bình của nhóm dữ liệu.
N là tổng số quan sát.

Tính giá trị trung bình của các quan sát trong từng nhóm. Để tính độ lệch chuẩn, đầu tiên bạn cần xác định giá trị trung bình (µ) của các quan sát trong mỗi nhóm. Cộng tất cả các giá trị quan sát và chia cho số lượng quan sát.

Ví dụ, xét nhóm sinh viên đọc tài liệu trước khi đến lớp với các điểm số: 90, 91, 85, 83 và 94.
Tổng các điểm số: 90 + 91 + 85 + 83 + 94 = 443.
Giá trị trung bình: 443 / 5 = 88.6.

Trừ từng giá trị quan sát cho giá trị trung bình. Bước này liên quan đến việc tính (x_i – µ). Lấy từng giá trị quan sát trừ đi giá trị trung bình đã tính.

Với ví dụ trên: (90 – 88.6) = 1.4, (91 – 88.6) = 2.4, (85 – 88.6) = -3.6, (83 – 88.6) = -5.6, (94 – 88.6) = 5.4.

Bình phương các hiệu số và cộng chúng lại. Bình phương từng hiệu số để loại bỏ dấu âm, sau đó cộng các kết quả lại.

Ví dụ: (1.4)² = 1.96, (2.4)² = 5.76, (-3.6)² = 12.96, (-5.6)² = 31.36, (5.4)² = 29.16.
Tổng: 1.96 + 5.76 + 12.96 + 31.36 + 29.16 = 81.2.

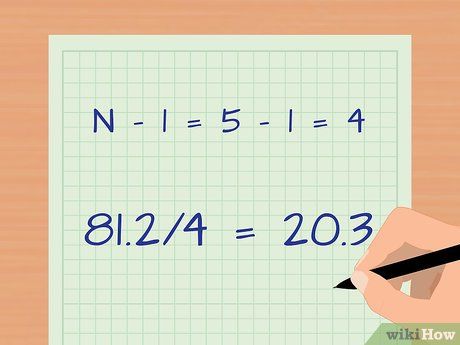
Chia tổng bình phương cho (N – 1). Điều này giúp điều chỉnh việc tính toán dựa trên mẫu thay vì toàn bộ tổng thể.

Ví dụ: 81.2 / (5 – 1) = 81.2 / 4 = 20.3.

Tính căn bậc hai của kết quả. Đây là bước cuối cùng để xác định độ lệch chuẩn.

Ví dụ: √20.3 ≈ 4.51.
Độ lệch chuẩn của nhóm sinh viên đọc tài liệu trước khi đến lớp là 4.51.

Xác định ý nghĩa thống kê giữa hai nhóm dữ liệu

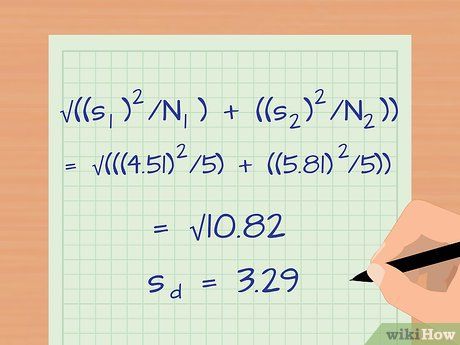
Tính phương sai giữa hai nhóm quan sát. Để so sánh hai nhóm, bạn cần tính phương sai dựa trên độ lệch chuẩn và kích thước mẫu của từng nhóm. Công thức tính phương sai là: s_d = √((s₁²/N₁) + (s₂²/N₂)).

s_d là phương sai giữa các nhóm.
s₁ và s₂ lần lượt là độ lệch chuẩn của nhóm 1 và nhóm 2.
N₁ và N₂ là kích thước mẫu của từng nhóm.
Ví dụ: s_d = √(((4.51)²/5) + ((5.81)²/5)) = √(4.07 + 6.75) = √10.82 = 3.29.

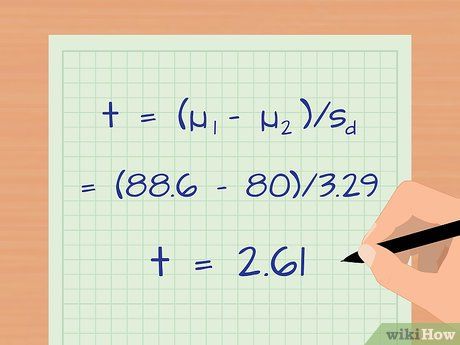
Tính giá trị thống kê t. Giá trị t giúp so sánh sự khác biệt giữa hai nhóm. Công thức tính là: t = (µ₁ – µ₂)/s_d.

µ₁ và µ₂ là giá trị trung bình của nhóm 1 và nhóm 2.
s_d là phương sai giữa các nhóm.
Ví dụ: t = (88.6 – 80)/3.29 = 2.61.

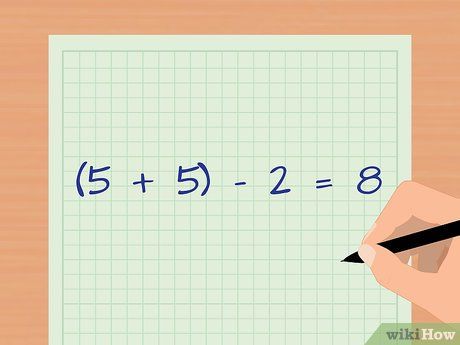
Xác định bậc tự do. Bậc tự do được tính bằng tổng số quan sát của cả hai nhóm trừ đi 2.

Ví dụ: (5 + 5) – 2 = 8.

Sử dụng bảng giá trị t để đánh giá ý nghĩa thống kê. Tra cứu bảng t với bậc tự do và giá trị t để tìm giá trị p.

Với bậc tự do 8 và t = 2.61, giá trị p nằm trong khoảng 0.01 đến 0.025.
Vì giá trị p nhỏ hơn 0.05, kết quả có ý nghĩa thống kê. Chúng ta bác bỏ giả thuyết không và chấp nhận giả thuyết nghịch: sinh viên đọc tài liệu trước khi đến lớp đạt điểm cao hơn.

Xem xét thực hiện nghiên cứu tiếp theo. Nhiều nhà nghiên cứu tiến hành các nghiên cứu tiền đề với một số phép đo để hiểu rõ hơn cách thiết kế một nghiên cứu quy mô lớn hơn. Việc thực hiện thêm các nghiên cứu với nhiều phép đo hơn sẽ giúp tăng cường độ tin cậy cho kết luận của bạn.

Lời khuyên hữu ích

Thống kê là một lĩnh vực rộng lớn và phức tạp. Hãy tham gia một khóa học về kiểm định giả thuyết thống kê ở trình độ trung học phổ thông, đại học hoặc cao hơn để nắm vững kiến thức về ý nghĩa thống kê.

Những điều cần lưu ý

Phân tích này tập trung vào kiểm định t để so sánh sự khác biệt giữa hai tổng thể có phân phối chuẩn. Tùy thuộc vào độ phức tạp của dữ liệu, bạn có thể cần sử dụng các phương pháp kiểm định thống kê khác phù hợp hơn.

Du lịch

Ẩm thực

Khám phá

Đi Phượt

Vẻ đẹp Việt Nam

Chuyến đi