Phương Pháp Tính Thể Tích
22/02/2025
Nội dung bài viết
Thể tích của một hình học là giá trị đo lường phần không gian ba chiều mà hình đó chiếm giữ. Bạn có thể hình dung thể tích như lượng chất lỏng (nước, không khí, cát,...) mà hình có thể chứa đựng khi được lấp đầy. Các đơn vị đo thể tích phổ biến bao gồm centimet khối (cm3), mét khối (m3), inch khối (in3), và feet khối (ft3). Bài viết này sẽ hướng dẫn bạn cách tính thể tích của 6 hình khối ba chiều thường gặp trong toán học, bao gồm hình lập phương, hình hộp chữ nhật, hình trụ, hình chóp, hình nón và hình cầu. Bạn sẽ nhận thấy các công thức tính thể tích có nhiều điểm tương đồng, giúp bạn dễ dàng ghi nhớ. Hãy cùng khám phá các bước chi tiết để hiểu rõ hơn nhé!
Các Bước Thực Hiện
Tính Thể Tích Hình Lập Phương
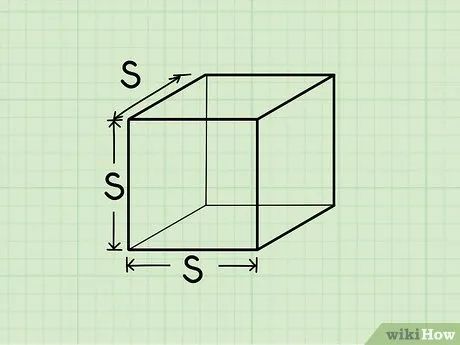
Nhận diện hình lập phương. Hình lập phương là một khối ba chiều với 6 mặt đều là hình vuông. Đây là một dạng hình hộp có tất cả các cạnh bằng nhau.
- Ví dụ thực tế về hình lập phương bao gồm viên xúc xắc 6 mặt, viên đường nén, hoặc các khối học chữ dành cho trẻ em.
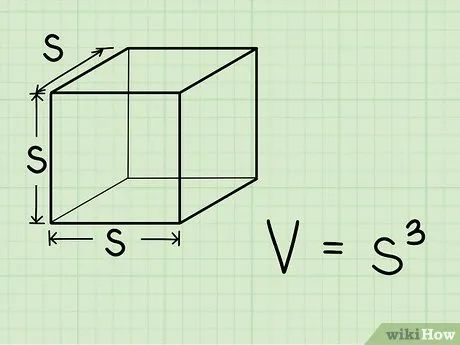
Công thức tính thể tích hình lập phương. Với các cạnh đều bằng nhau, công thức tính thể tích hình lập phương trở nên vô cùng đơn giản: V = s3, trong đó V là thể tích và s là độ dài cạnh của hình lập phương.
- Để tính s3, bạn chỉ cần nhân s với chính nó ba lần: s3 = s * s * s.
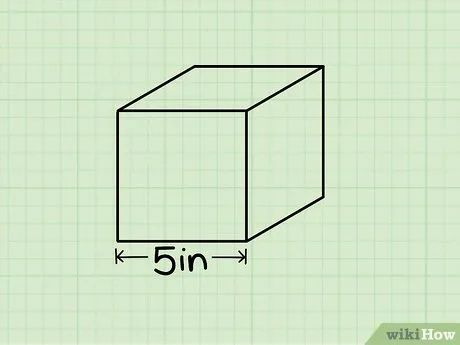
Xác định chiều dài cạnh của hình lập phương. Tùy vào bài toán, độ dài cạnh có thể được cung cấp sẵn hoặc bạn cần tự đo bằng thước. Vì tất cả các cạnh của hình lập phương đều bằng nhau, bạn chỉ cần đo một cạnh duy nhất.
- Nếu không chắc chắn hình khối bạn đang đo có phải là hình lập phương hay không, hãy đo tất cả các cạnh. Nếu chúng không bằng nhau, hãy áp dụng công thức tính thể tích hình hộp chữ nhật.
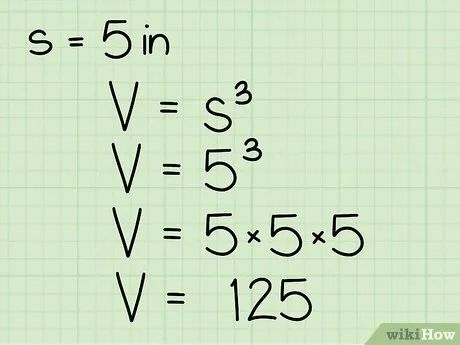
Thay giá trị cạnh vào công thức V = s3 và tính toán. Ví dụ, nếu cạnh hình lập phương là 5 inches, ta có: V = (5 in)3. Kết quả là 5 in * 5 in * 5 in = 125 in3, chính là thể tích của hình lập phương.
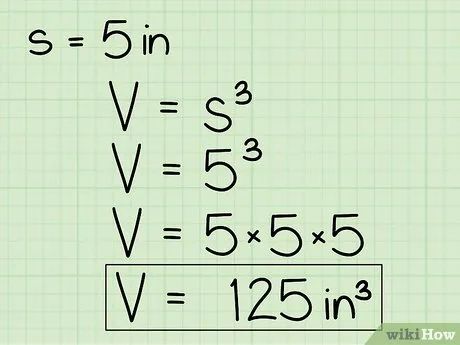
Đảm bảo đơn vị đo thể tích được viết dưới dạng khối (mũ 3). Trong ví dụ trên, cạnh được đo bằng inch nên thể tích có đơn vị là inch khối. Nếu cạnh là 3 cm, thể tích sẽ là V = (3 cm)3, tương đương 27 cm3.
Tính Thể Tích Hình Hộp Chữ Nhật
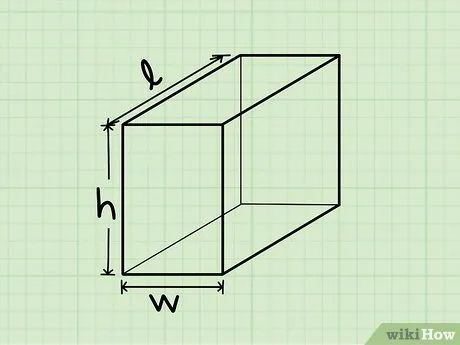
Nhận diện hình hộp chữ nhật. Hình hộp chữ nhật, hay còn gọi là lăng kính chữ nhật, là một khối ba chiều với 6 mặt đều là hình chữ nhật. Đây là một hình chữ nhật được mở rộng trong không gian ba chiều, hoặc đơn giản là một hình hộp.
- Hình lập phương là một trường hợp đặc biệt của hình hộp chữ nhật khi tất cả các cạnh có độ dài bằng nhau.
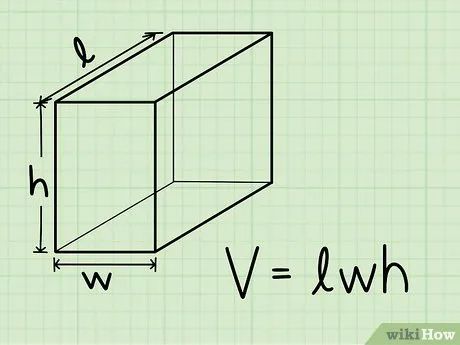
Công thức tính thể tích. Thể tích của hình hộp chữ nhật được tính bằng công thức: Thể tích = chiều dài (l) * chiều rộng (w) * chiều cao (h), hay V = lwh.
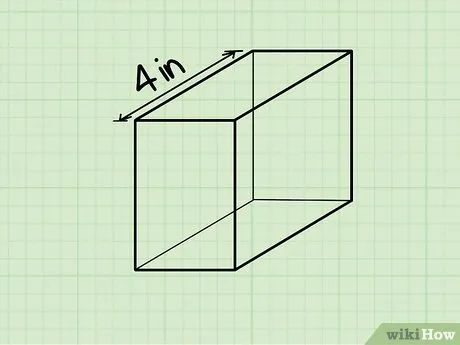
Xác định chiều dài của hình hộp chữ nhật. Chiều dài là cạnh dài nhất của mặt hình hộp nằm song song với mặt phẳng đặt hình. Chiều dài có thể được cung cấp trong đề bài hoặc bạn cần đo bằng thước.
- Ví dụ, nếu chiều dài là 4 inches, thì l = 4 in.
- Bạn không cần quá lo lắng về việc phân biệt chiều dài, chiều rộng hay chiều cao. Miễn là bạn có ba giá trị khác nhau, kết quả cuối cùng sẽ không thay đổi dù bạn sắp xếp chúng thế nào.
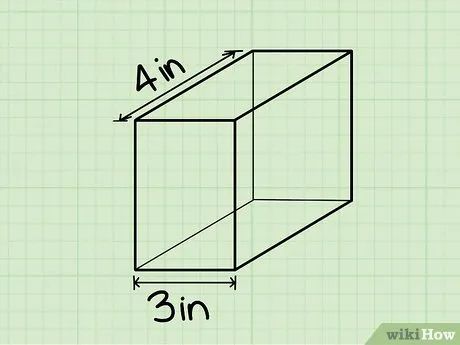
Xác định chiều rộng của hình hộp chữ nhật. Chiều rộng là cạnh ngắn hơn của mặt song song với mặt phẳng đặt hình. Bạn có thể tìm giá trị này từ biểu đồ hoặc đo bằng thước.
- Ví dụ, nếu chiều rộng là 3 inches, thì w = 3 in.
- Hãy đảm bảo sử dụng cùng một đơn vị đo cho tất cả các cạnh. Đừng kết hợp inch và centimet trong cùng một phép tính.
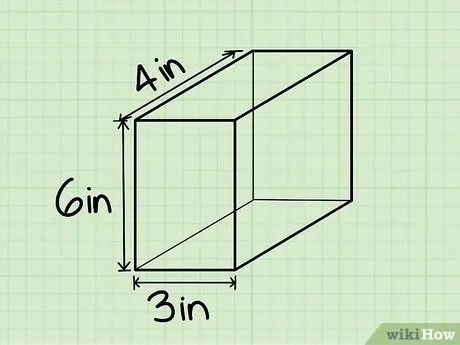
Xác định chiều cao của hình hộp chữ nhật. Chiều cao là khoảng cách từ mặt đáy đến mặt trên của hình hộp. Bạn có thể xác định giá trị này từ biểu đồ hoặc đo bằng thước.
- Ví dụ, nếu chiều cao là 6 inches, thì h = 6 in.
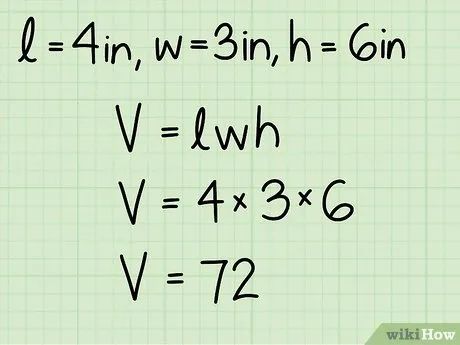
Thay các giá trị vào công thức tính thể tích hình hộp chữ nhật: V = lwh.
- Với các ví dụ trên, l = 4 in, w = 3 in, h = 6 in. Do đó, V = 4 * 3 * 6 = 72.
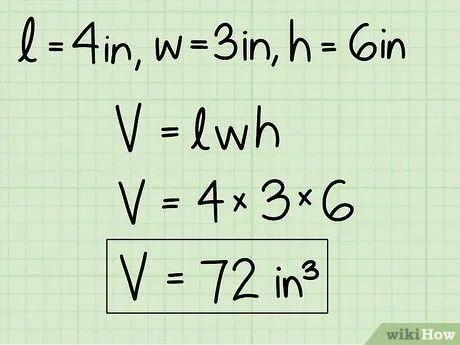
Đảm bảo kết quả được biểu thị dưới dạng khối (mũ 3 của đơn vị đo). Vì các cạnh được đo bằng inch, thể tích của hình hộp chữ nhật là 72 in3.
- Ví dụ khác: nếu l = 2 cm, w = 4 cm, h = 8 cm, thể tích sẽ là 2 cm * 4 cm * 8 cm = 64 cm3.
Tính Thể Tích Hình Trụ Tròn
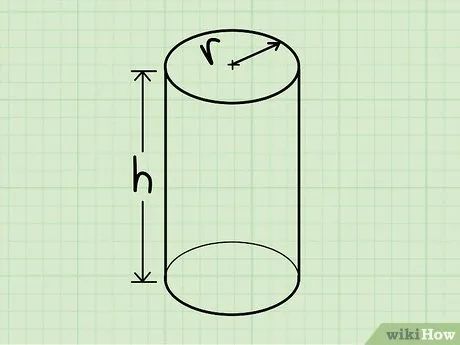
Nhận diện hình trụ. Hình trụ là một khối không gian có hai đáy phẳng là hình tròn giống nhau và một mặt cong kết nối hai đáy.
- Ví dụ thực tế: pin AA hoặc pin AAA thường có hình trụ tròn.
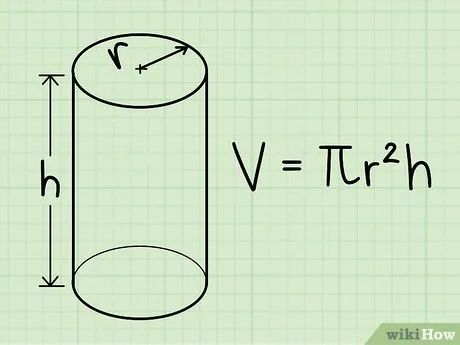
Công thức tính thể tích hình trụ tròn. Để tính thể tích, bạn cần biết chiều cao (h) và bán kính đáy (r). Công thức là: V = πr2h, trong đó π là hằng số pi.
- Trong nhiều trường hợp, π có thể được làm tròn thành 3,14. Hãy tham khảo ý kiến giáo viên để biết cách sử dụng phù hợp.
- Công thức này tương tự như tính thể tích hình hộp chữ nhật, nhưng diện tích đáy được thay bằng πr2.
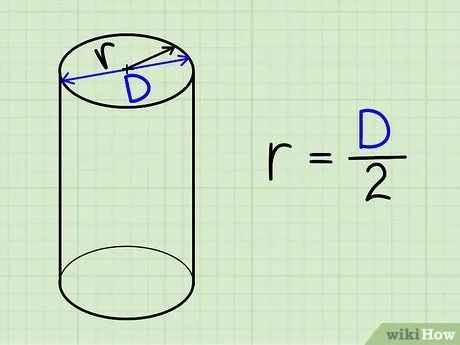
Xác định bán kính mặt đáy. Nếu giá trị này được cung cấp trong giản đồ, bạn có thể sử dụng trực tiếp. Nếu đề bài cho đường kính (d), bạn chỉ cần chia đôi giá trị này để tìm bán kính (vì d = 2r).
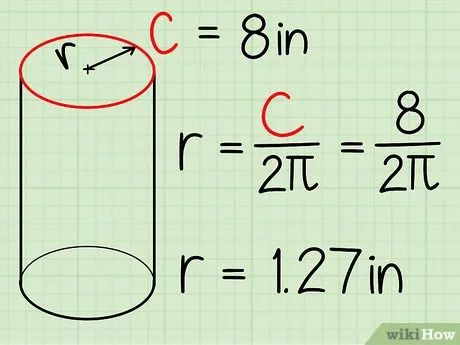
Đo đạc để tìm bán kính mặt đáy. Để đo bán kính, bạn có thể đo phần rộng nhất của mặt đáy và chia đôi. Hoặc, đo chu vi mặt đáy và áp dụng công thức C = 2πr để tính bán kính.
- Ví dụ, nếu chu vi là 8 inches, bán kính sẽ là 1,27 in.
- Phương pháp đo chu vi thường cho kết quả chính xác hơn. Hãy kiểm tra lại nếu có sự chênh lệch lớn giữa hai phương pháp.
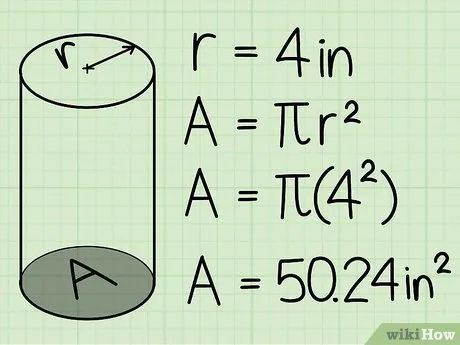
Tính diện tích mặt đáy của hình trụ. Sử dụng công thức πr2. Nhân bán kính với chính nó, sau đó nhân với π. Ví dụ:
- Nếu bán kính là 4 inches, diện tích mặt đáy là A = π * 42 = 50,24 in2.
- Nếu biết đường kính, hãy chia đôi để tìm bán kính trước khi tính toán.
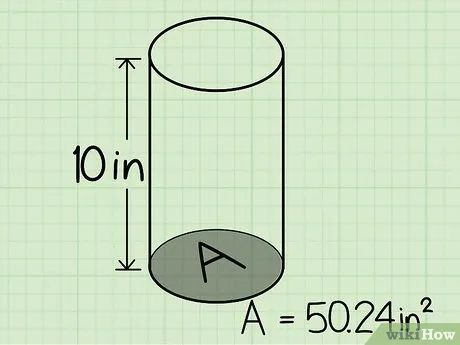
Xác định chiều cao của hình trụ. Chiều cao là khoảng cách giữa hai mặt đáy. Bạn có thể tìm giá trị này trên giản đồ hoặc đo trực tiếp bằng thước.

Tính thể tích hình trụ. Nhân diện tích mặt đáy với chiều cao hoặc sử dụng công thức V = πr2h. Ví dụ:
- Với bán kính 4 inches và chiều cao 10 inches, V = π * 42 * 10 = 502,4 in3.

Kết quả thể tích cần được biểu thị theo đơn vị khối (mũ 3). Trong ví dụ trên, hình trụ được đo bằng inch nên thể tích là 502,4 in3. Nếu hình trụ được đo bằng centimet, thể tích sẽ được tính bằng centimet khối (cm3).
Tính Thể Tích Hình Chóp
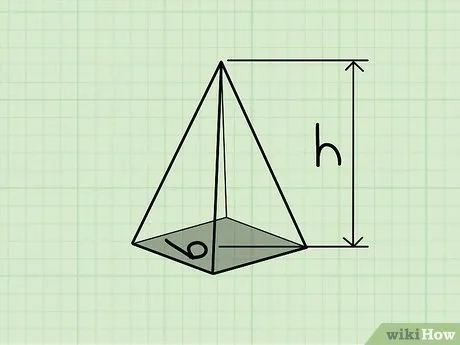
Nhận diện hình chóp. Hình chóp là một khối không gian có đáy là đa giác và các mặt bên giao nhau tại đỉnh. Hình chóp đa giác đều có đáy là đa giác đều, với các cạnh và góc bằng nhau.
- Hình chóp thường được hình dung với đáy là hình vuông, nhưng đáy có thể có 5, 6, hoặc thậm chí 100 cạnh.
- Hình chóp có đáy là hình tròn được gọi là hình nón, sẽ được đề cập sau.
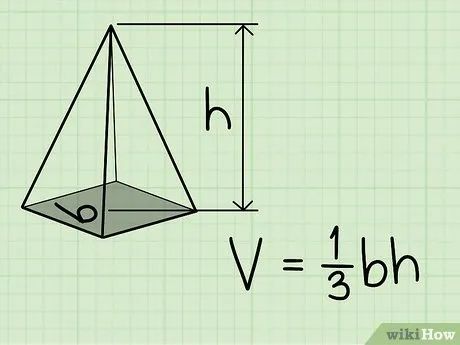
Công thức tính thể tích hình chóp đa giác đều. Công thức là V = 1/3bh, trong đó b là diện tích đáy và h là chiều cao từ đỉnh đến mặt đáy.
- Công thức này áp dụng cho cả hình chóp đều và hình chóp xiên, với hình chiếu của đỉnh xuống đáy có thể không phải là tâm.
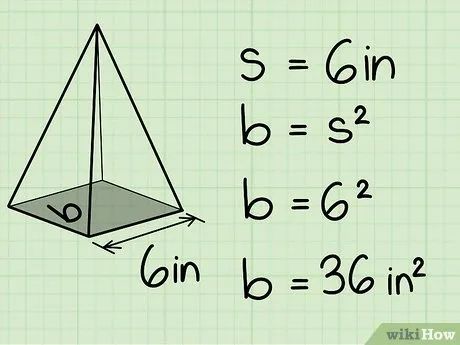
Tính diện tích mặt đáy. Diện tích đáy phụ thuộc vào hình dạng đa giác. Ví dụ, với đáy là hình vuông cạnh 6 inches, diện tích là A = s2 = 36 in2.
- Đối với đáy là tam giác, công thức là A = 1/2bh.
- Diện tích đa giác bất kỳ có thể tính bằng A = 1/2pa, với p là chu vi và a là trung đoạn.
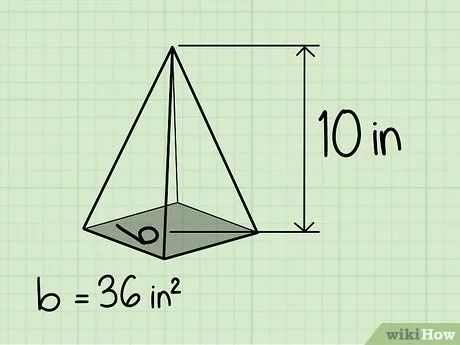
Xác định chiều cao của hình chóp. Trong hầu hết trường hợp, chiều cao được cung cấp trong giản đồ. Ví dụ, chiều cao của hình chóp là 10 inches.
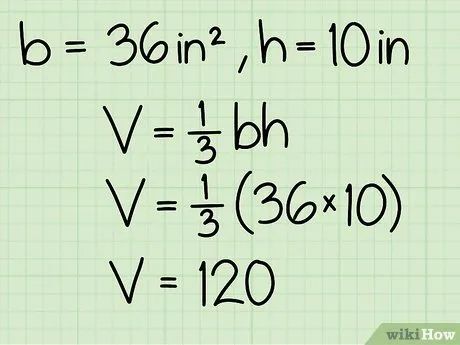
Tính thể tích hình chóp. Nhân diện tích đáy với chiều cao, sau đó chia cho 3 theo công thức V = 1/3bh. Ví dụ, với diện tích đáy 36 và chiều cao 10, thể tích là 36 * 10 * 1/3 = 120.
- Với hình chóp có đáy là ngũ giác diện tích 26 và chiều cao 8, thể tích là 1/3 * 26 * 8 = 69,33.
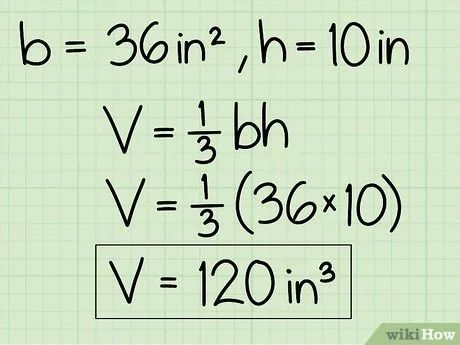
Biểu thị kết quả theo đơn vị khối (mũ 3). Trong ví dụ trên, hình chóp được đo bằng inch nên thể tích là 120 in3. Nếu đo bằng mét, thể tích sẽ là m3.
Tính Thể Tích Hình Nón
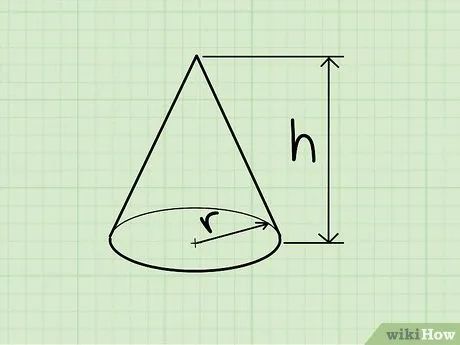
Đặc điểm của hình nón. Hình nón là khối không gian ba chiều với đáy là hình tròn và một đỉnh duy nhất. Bạn có thể hình dung nó như một hình chóp có đáy tròn.
- Nếu đỉnh chiếu xuống tâm đáy, đó là hình nón đều. Ngược lại, là hình nón xiên. Công thức tính thể tích của cả hai là giống nhau.
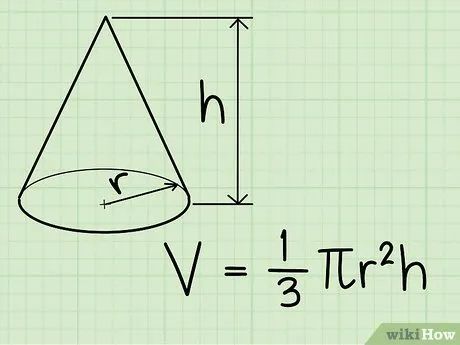
Công thức tính thể tích hình nón. V = 1/3πr2h, trong đó r là bán kính đáy, h là chiều cao, và π là hằng số pi (có thể làm tròn thành 3,14).
- Phần πr2 chính là diện tích đáy, cho thấy công thức này tương tự như công thức tính thể tích hình chóp: 1/3bh.
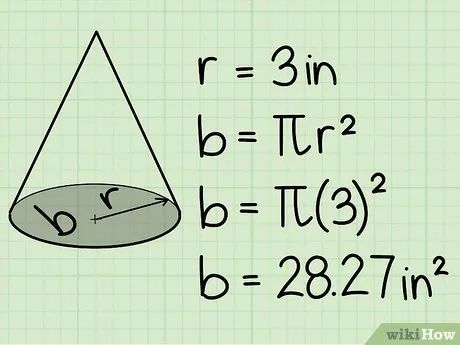
Tính diện tích mặt đáy của hình nón. Để tính diện tích, xác định bán kính đáy (r). Nếu đề bài cho đường kính, chia đôi để có bán kính. Sau đó áp dụng công thức A = πr2.
- Ví dụ, với bán kính 3 inches, A = π * 32 = 9π ≈ 28,27 in2.
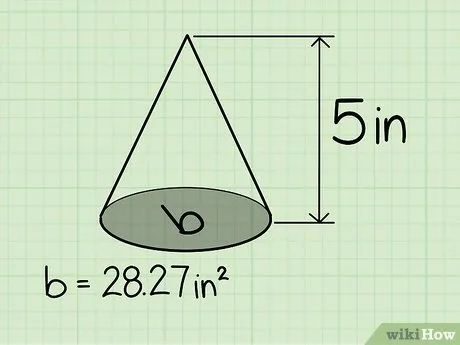
Xác định chiều cao của hình nón. Chiều cao là khoảng cách từ đỉnh đến mặt đáy. Trong ví dụ này, chiều cao là 5 inches.
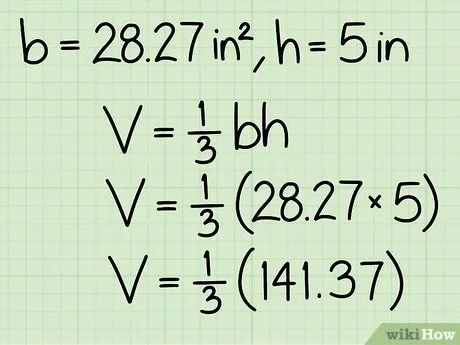
Nhân diện tích đáy với chiều cao. Với diện tích đáy 28,27 in2 và chiều cao 5 in, ta có bh = 28,27 * 5 = 141,35.

Tính thể tích hình nón. Nhân kết quả trên với 1/3 (hoặc chia cho 3). Trong ví dụ này, thể tích là 141,35 * 1/3 = 47,12.
- Công thức rút gọn: 1/3π * 32 * 5 = 47,12.
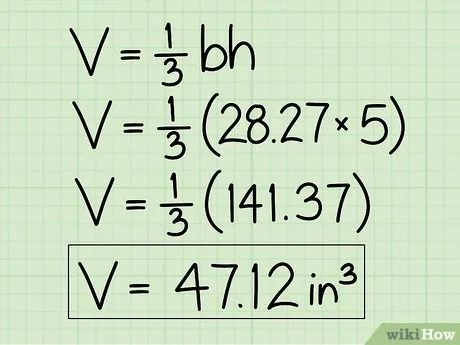
Ghi đúng đơn vị thể tích. Trong ví dụ trên, các giá trị được đo bằng inch, vì vậy thể tích cần được ghi là 47,12 in3.
Tính Thể Tích Hình Cầu
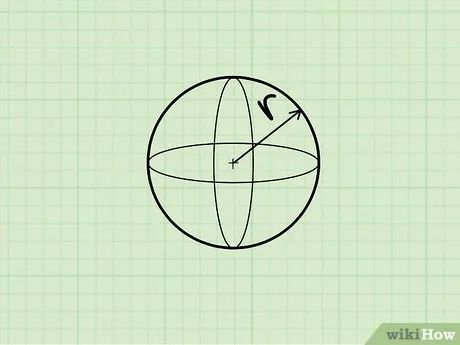
Nhận diện hình cầu. Hình cầu là một vật thể tròn hoàn hảo, với mọi điểm trên bề mặt cách đều tâm một khoảng không đổi. Nói cách khác, hình cầu giống như một quả bóng.
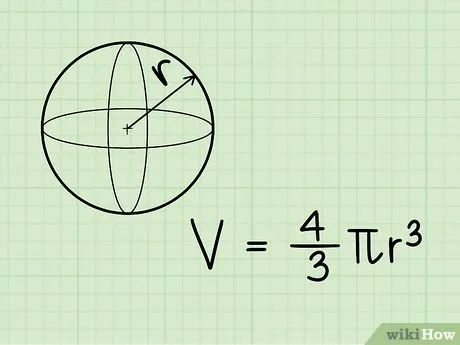
Công thức tính thể tích hình cầu. Công thức là V = 4/3πr3, trong đó r là bán kính và π là hằng số pi (3,14).
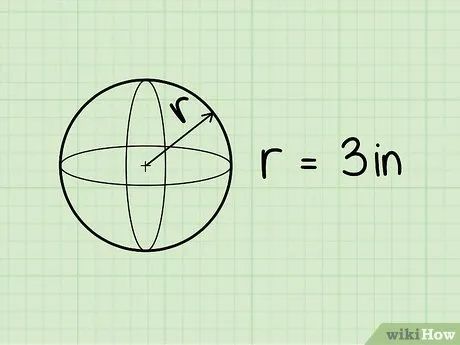
Xác định bán kính của hình cầu. Nếu bán kính được cho sẵn, hãy sử dụng giá trị đó. Nếu đề bài cho đường kính, chia đôi để tìm bán kính. Ví dụ, bán kính hình cầu trong giản đồ là 3 inches.
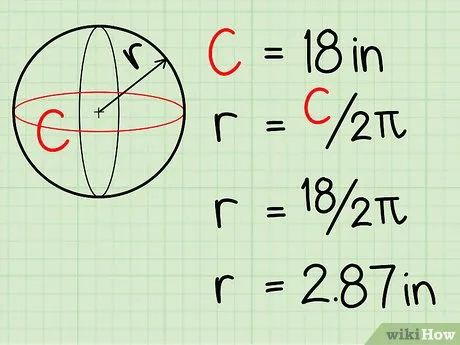
Đo bán kính nếu chưa biết giá trị. Để đo bán kính hình cầu, dùng dây cuốn quanh phần rộng nhất và đo chu vi. Chia chu vi cho 2π (hoặc 6,28) để tìm bán kính.
- Ví dụ, nếu chu vi là 18 inches, bán kính là 18 / 6,28 ≈ 2,87 in.
- Để tăng độ chính xác, đo 3 lần và lấy giá trị trung bình. Ví dụ, nếu chu vi đo được là 18, 17,75, và 18,2 inches, giá trị trung bình là (18 + 17,75 + 18,2) / 3 ≈ 17,98 inches.
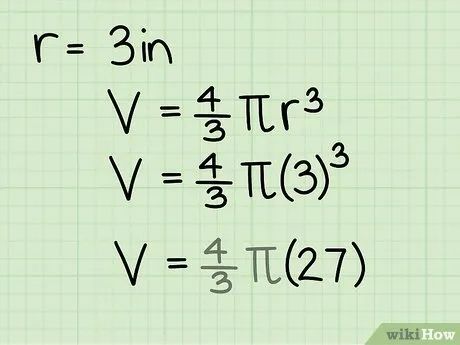
Tính lũy thừa bậc ba của bán kính (r3). Nhân bán kính với chính nó ba lần. Ví dụ, với r = 3, ta có r3 = 3 * 3 * 3 = 27.
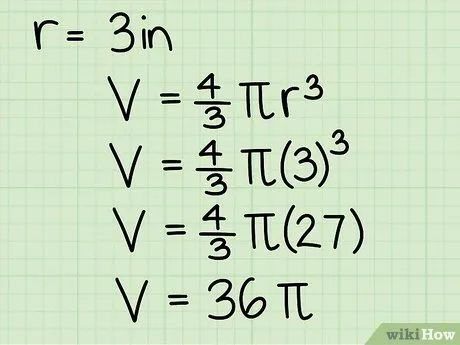
Nhân kết quả với 4/3. Ví dụ, 27 * 4/3 = 36.

Nhân kết quả với π để tính thể tích hình cầu. Làm tròn π thành 3,14. Ví dụ, 36 * 3,14 = 113,04.

Ghi kết quả theo đơn vị khối. Trong ví dụ này, bán kính được đo bằng inch nên thể tích là 113,04 in3.
Du lịch
Ẩm thực
Khám phá
Đi Phượt
Vẻ đẹp Việt Nam
Chuyến đi
Có thể bạn quan tâm

Top 7 loại băng vệ sinh tampon chất lượng hàng đầu dành cho phái đẹp

Khám phá công thức kho quẹt rau củ của chị Thuý Hằng, một món ăn không chỉ ngon mà còn đơn giản, phù hợp cho bữa cơm gia đình.

3 Địa điểm massage người khiếm thị chất lượng và đáng tin cậy nhất tại Đà Lạt

5 Địa điểm đáng tin cậy nhất để mua máy sưởi cao cấp tại Tuyên Quang

Những hình ảnh tuyệt đẹp nhất về Thủy Thủ Mặt Trăng Pha Lê


