10 công thức hình học cơ bản nhất bậc tiểu học kèm bài tập minh họa chi tiết
Nội dung bài viết
1. Khám phá hình thoi
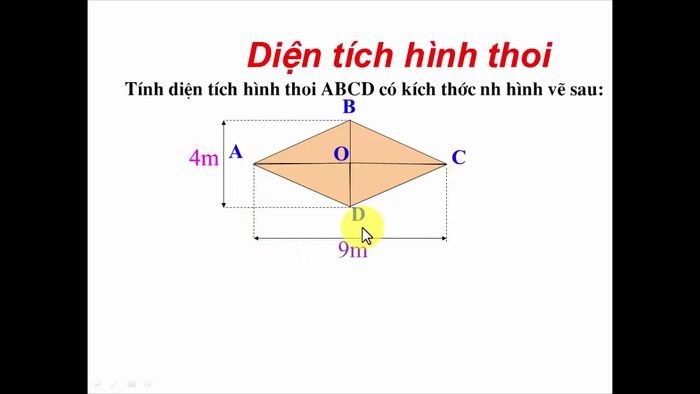
Hình thoi - tứ giác đặc biệt với 4 cạnh bằng nhau, sở hữu những tính chất ấn tượng: hai góc đối bằng nhau, hai đường chéo vuông góc cắt nhau tại trung điểm mỗi đường đồng thời là đường phân giác các góc. Hình thoi còn kế thừa mọi tính chất của hình bình hành.
Công thức quan trọng:
- Diện tích: S = ½ (m × n) (m, n: độ dài hai đường chéo)
- Tích hai đường chéo: m × n = 2S
2. Khám phá hình tam giác đa diện
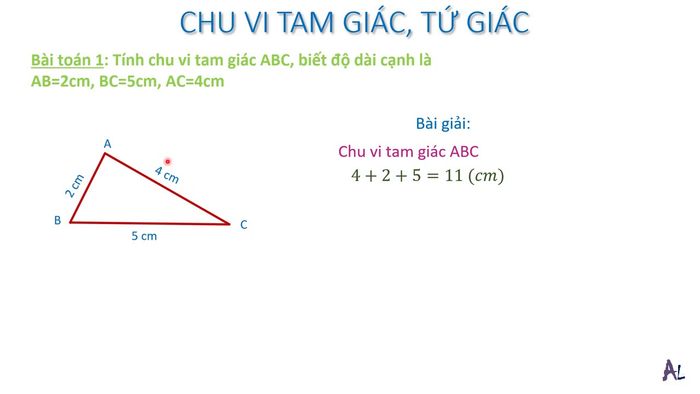
Hình tam giác - kiến trúc cơ bản của hình học phẳng, được tạo thành từ ba đỉnh không thẳng hàng nối với nhau bằng ba cạnh thẳng. Là đa giác tối giản nhất với 3 cạnh, tam giác luôn giữ nguyên tính đơn giản và độ lồi hoàn hảo (mọi góc trong đều nhỏ hơn 180°).
Bộ công thức vàng:
- Chu vi: P = a + b + c (tổng ba cạnh)
- Diện tích: S = ½ (a × h) (cạnh đáy nhân chiều cao tương ứng)
- Chiều cao: h = 2S ÷ a
- Cạnh đáy: a = 2S ÷ h
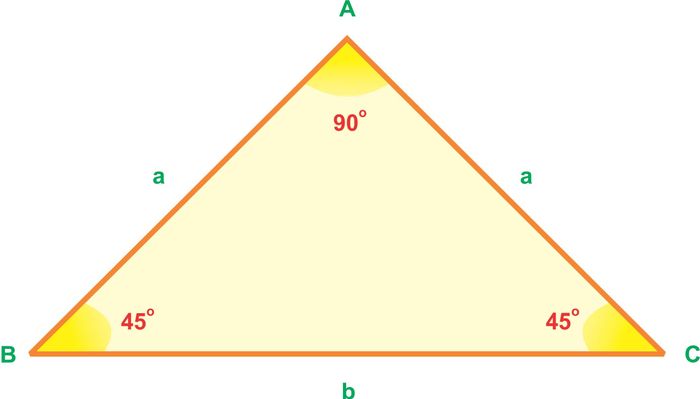
3. Đặc biệt: Tam giác vuông vàng
Công thức diện tích tinh gọn: S = ½ × a² (với a là độ dài cạnh góc vuông)
4. Bí quyết tính toán hình thang
Hình thang - tứ giác đặc biệt với hai cạnh đáy song song, là nền tảng quan trọng trong hình học. Khám phá các dạng đặc biệt:
- Hình thang vuông: Sở hữu một góc 90° hoàn hảo
- Hình thang cân: Hai góc kề đáy bằng nhau tạo sự cân đối
- Hình thang vuông cân: Sự kết hợp hoàn hảo giữa vuông góc và cân đối
Công thức vàng cho hình thang:
- Diện tích: S = ½ × (a + b) × h (a, b: hai đáy)
- Chiều cao: h = 2S ÷ (a + b)
- Tổng hai đáy: a + b = 2S ÷ h
- Chu vi: P = tổng 4 cạnh (a + b + c + d)
- Tìm đáy lớn/nhỏ: Lấy tổng hai đáy trừ đi đáy còn lại

5. Bí mật hình tròn - Vòng tròn hoàn hảo
Hình tròn - kiệt tác hình học với mọi điểm cách đều tâm, tạo nên vẻ đẹp cân đối tuyệt đối. Được xác định bởi đường tròn bao quanh, hình tròn có thể là đóng hoặc mở tùy theo việc chứa đường biên hay không.
Công thức vàng cho hình tròn:
- Bán kính: r = d/2 = C/(2π)
- Đường kính: d = 2r = C/π
- Chu vi: C = 2πr = πd
- Diện tích: S = πr²
- Diện tích hình vành khăn: S = π(R² - r²)
- Bán kính lớn: R = r + chiều rộng vành

6. Bí quyết tính toán hình hộp chữ nhật
Công thức cơ bản:
- Diện tích xung quanh: Sxq = Chu vi đáy × Chiều cao
- Chu vi đáy: P = (a + b) × 2 (hình chữ nhật) hoặc P = a × 4 (hình vuông)
- Diện tích toàn phần: Stp = Sxq + 2 × Sđáy
- Thể tích: V = a × b × c
Ứng dụng thực tế:
- Tính chiều cao hồ nước: h = V ÷ Sđáy
- Tính diện tích đáy: Sđáy = V ÷ h
- Chiều cao mặt nước: hnước = Vnước ÷ Sđáy
- Chiều cao phần trống: htrống = htổng - hnước
Cách tính diện tích quét vôi:
- Tính diện tích tường (Sxq)
- Tính diện tích trần (a × b)
- Tổng diện tích cần quét = (Sxq + Strần) - Scửa

7. Bí mật hình lập phương - Khối vuông hoàn hảo
Công thức vàng cho hình lập phương:
- Diện tích xung quanh: Sxq = 4 × a² (4 mặt bên bằng nhau)
- Độ dài cạnh: a = √(Sxq ÷ 4)
- Diện tích toàn phần: Stp = 6 × a² (6 mặt vuông đều)
- Độ dài cạnh: a = √(Stp ÷ 6)
- Thể tích: V = a³ (chiều dài × chiều rộng × chiều cao)

8. Hình vuông - Sự hoàn hảo của các cạnh bằng nhau
Hình vuông - tứ giác hoàn hảo với 4 cạnh bằng nhau và 4 góc vuông, kết hợp tinh hoa của hình chữ nhật, hình thoi và hình thang. Đặc điểm nổi bật: đường chéo vuông góc tại trung điểm, các cặp cạnh đối song song hoàn hảo.
Công thức cốt lõi:
- Chu vi: P = 4a
- Cạnh: a = P/4
- Diện tích: S = a²
Quy luật thú vị:
Bài tập minh họa:
- Ví dụ 1: Hình vuông chu vi 32cm → Diện tích 64cm²
- Ví dụ 2: Mở rộng 1 phía 8m → Diện tích mới 825m²
- Ví dụ 3: Mở rộng mỗi cạnh 4m → Diện tích gốc 676m²

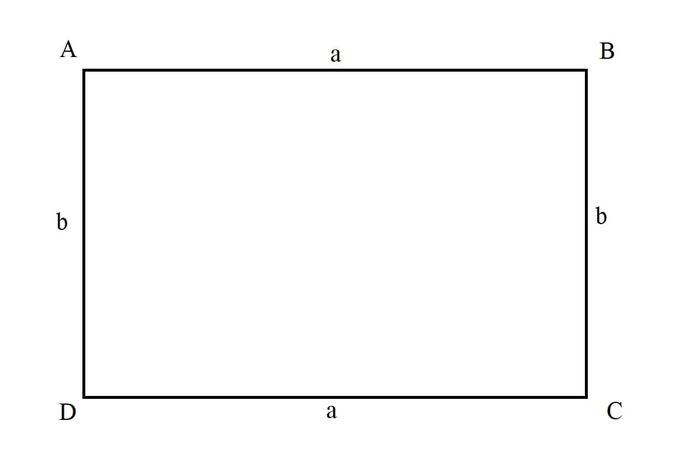
9. Hình chữ nhật - Tứ giác vuông cân đối
Hình chữ nhật - tứ giác 4 góc vuông, đồng thời là hình bình hành và hình thang cân đặc biệt.
Công thức cơ bản:
- Chu vi: P = 2(a + b)
- Chiều dài/rộng: a = P/2 - b, b = P/2 - a
- Diện tích: S = a × b
Bài tập ứng dụng:
- Cơ bản: Tính chu vi 90cm và diện tích 500cm² khi biết 2 cạnh
- Nâng cao: Bài toán giảm chiều rộng 6cm làm diện tích giảm 120cm²
- Thực tế: Tính chu vi mảnh đất khi thay đổi kích thước thành hình vuông
Bài tập phát triển:
- So sánh 3 lần chiều rộng với 2 lần chiều dài
- Mối quan hệ giữa hình vuông và hình chữ nhật
- Tỉ lệ chu vi và chiều rộng
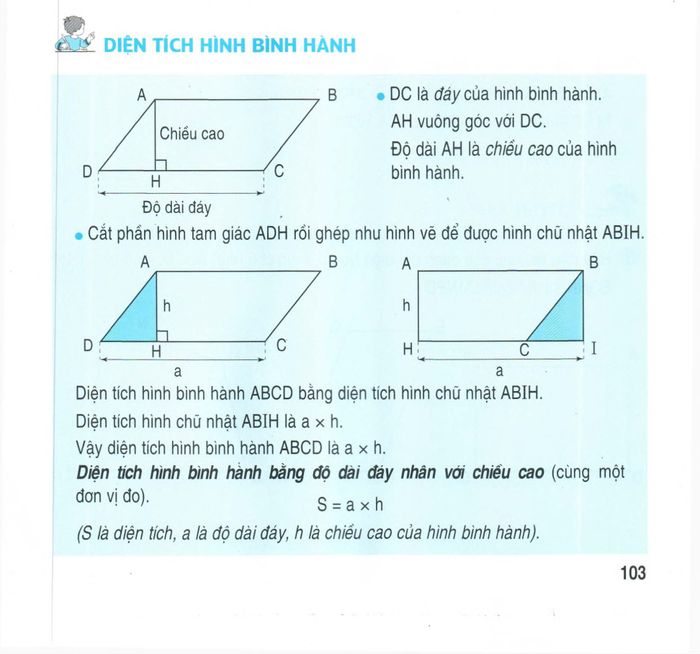
10. Hình bình hành - Tứ giác song song đặc biệt
Hình bình hành - tứ giác đặc biệt với hai cặp cạnh đối song song hoặc một cặp cạnh đối song song và bằng nhau. Sở hữu các tính chất: góc đối bằng nhau, đường chéo cắt tại trung điểm, là trường hợp đặc biệt của hình thang.
Công thức cốt lõi:
- Chu vi: P = 2(a + b)
- Diện tích: S = a × h
- Độ dài đáy/chiều cao: a = S/h, h = S/a
Bài tập ứng dụng:
- Cơ bản: Tính diện tích 75cm² khi biết chiều cao 5cm và cạnh 15cm
- Mở rộng: Tính diện tích ban đầu 1269m² khi tăng cạnh đáy 7m
- Tổng hợp: Tính diện tích 5000cm² từ chu vi 480cm với tỉ lệ cạnh đặc biệt
Có thể bạn quan tâm

Top 6 Sản phẩm điều trị ho cho trẻ sơ sinh an toàn và hiệu quả nhất

Giá tiêu hôm nay 12/03/2024: Mức giá duy trì ổn định, đạt mức cao nhất 95.000 đồng/kg.

Top 10 TV Samsung trên 50 inch màn hình siêu nét đáng đầu tư nhất hiện nay

Top 8 Quán trà sữa nổi tiếng và ngon nhất tại Bàu Cát, Tân Bình, TP. HCM

9x chia sẻ bí kíp làm chả cá chép bằng máy xay sinh tố – chả dai giòn, thơm ngon chuẩn vị, không hề bị bở


