Bí quyết tính diện tích hình thoi đơn giản và chính xác

Hình thoi là tứ giác đặc biệt với 4 cạnh bằng nhau, hai cặp cạnh đối song song hoàn hảo, các góc đối xứng bằng nhau (không vuông), hai đường chéo vuông góc và cắt nhau tại trung điểm. Có thể hiểu đơn giản: hình thoi chính là hình bình hành đặc biệt khi có hai cạnh kề bằng nhau. Sau đây chúng ta sẽ khám phá công thức tính diện tích hình thoi kèm các bài tập minh họa thực tế.

Công thức vàng tính diện tích hình thoi

PHƯƠNG PHÁP TÍNH DIỆN TÍCH HÌNH THOI CHUẨN XÁC

Công thức chuẩn: S = ½ × d₁ × d₂ (Diện tích bằng nửa tích hai đường chéo, đơn vị mét vuông - m²) - Áp dụng dễ dàng trong mọi bài toán thực tế.

Để tính chính xác diện tích hình thoi, bạn chỉ cần xác định độ dài hai đường chéo. Cùng thực hành qua các bài tập minh họa sau.

Bài tập 1: Cho hình thoi có đường chéo d₁ = 5cm, đường chéo d₂ có độ dài gấp đôi d₁. Hãy tính diện tích hình thoi.

Lời giải:

Theo đề bài, d₁ = 5cm → d₂ = 2 × d₁ = 10cm. Đây chính là hai yếu tố cần thiết để tính diện tích.

Áp dụng công thức vàng: S = ½ × d₁ × d₂ = ½ × 5 × 10 = 25cm² - Kết quả chính xác và dễ hiểu.

Bài tập nâng cao: Tính diện tích hình thoi khi biết cạnh a = 7cm, đường chéo d₂ = 6cm và đường cao AH = 5cm trong tam giác cân ABC.

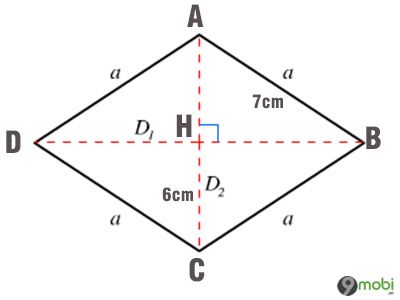
Lời giải chi tiết:

Bước đầu tiên để giải bài toán này là xác định độ dài đường chéo còn thiếu.

Áp dụng tính chất đặc trưng của hình thoi: hai đường chéo vuông góc và cắt nhau tại trung điểm mỗi đường. Với AH = 5cm, ta suy ra đường chéo d₁ = 10cm.

Áp dụng công thức vàng: S = ½ × d₁ × d₂ = ½ × 10 × 6 = 30cm²

Kết quả cuối cùng: Diện tích hình thoi là 30cm²

Ở các cấp học cao hơn, chúng ta sẽ khám phá thêm nhiều phương pháp tính diện tích hình thoi thú vị khác thông qua định lý Pytago và các công thức lượng giác, mở ra những cách tiếp cận mới đầy bất ngờ.

Bài viết đã hệ thống hóa kiến thức cơ bản về hình thoi một cách dễ hiểu. Nếu bạn gặp bất kỳ bài toán nào liên quan đến chu vi hay diện tích hình thoi, đừng ngần ngại để lại bình luận để được hỗ trợ giải đáp chi tiết.

https://Tripi.vn/cach-tinh-dien-tich-hinh-thoi-25348n.aspx
Khám phá thế giới hình học: Hình thoi, hình vuông và hình bình hành đều là những trường hợp đặc biệt của tứ giác, mỗi loại mang công thức tính diện tích riêng biệt tùy thuộc vào tính chất đặc trưng của chúng.